Symboles & Patterns – Essai sur l'intelligence et la créativité


Je dis qu'il faut être voyant, se faire voyant. Le Poète se fait voyant par un long, immense et raisonné dérèglement de tous les sens. Toutes les formes d'amour, de souffrance, de folie ; il cherche lui-même, il épuise en lui tous les poisons, pour n'en garder que les quintessences. Ineffable torture où il a besoin de toute la foi, de toute la force surhumaine, où il devient entre tous le grand malade, le grand criminel, le grand maudit, -- et le suprême Savant ! -- Car il arrive à l'inconnu ! Puisqu'il a cultivé son âme, déjà riche, plus qu'aucun ! Il arrive à l'inconnu, et quand, affolé, il finirait par perdre l'intelligence de ses visions, il les a vues ! [...] [...] Donc le poète est vraiment voleur de feu. Il est chargé de l'humanité, des animaux même; il devra faire sentir, palper, écouter ses inventions; si ce qu'il rapporte de là-bas a forme, il donne forme: si c'est informe, il donne de l'informe. Trouver une langue ; – Du reste, toute parole étant idée, le temps d'un langage universel viendra ! [...] Des faibles se mettraient à penser sur la première lettre de l'alphabet qui pourraient vite se ruer dans la folie ! – Cette langue sera de l'âme pour l'âme, résumant tout, parfums, sons, couleurs de la pensée accrochant la pensée et tirant. Le poète définirait la quantité d'inconnu s'éveillant en son temps dans l'âme universelle [...] Énormité devenue norme, absorbée par tous, il serait vraiment un multiplicateur de progrès ! Arthur Rimbaud, Lettre à Paul Dumény (1871)
Cet essai est une tentative de proposer un formalisme qui pourrait s'appliquer à toute discipline ou tout domaine de la connaissance humaine. Mon parcours m'a en effet progressivement conduit à percevoir une profonde unité dans la façon dont les savoirs se construisent et se transmettent. Je souhaitais donc rendre explicites ces analogies en mettant en lumière ce que tous les systèmes de représentation, qu'ils soient mathématiques, linguistiques, artistiques ou autres, ont en commun.

La genèse de ce texte remonte à l'époque où je venais tout juste d'être diplômé. Pour la première fois, je me retrouvais face à une page blanche, sans horizon tout tracé devant moi. Fort de ma formation d'ingénieur, j'étais versé dans les mathématiques, la physique, la programmation, l'intelligence artificielle et même les neurosciences. Par ailleurs, je nourrissais une passion pour l'esprit critique, la philosophie des sciences, la logique formelle et surtout la musique. Mon parcours m'avait déjà fait pressentir les incroyables correspondances qui pouvaient exister entre ces différentes disciplines, mais un évènement marquant survenu quelques mois plus tôt avait agi comme un catalyseur : une expérience de vie intense dont avaient émergé de nouvelles idées concernant les patterns, l'intelligence et la créativité. Ce fut le point de départ pour explorer ces perspectives nouvelles, et je décidai de me lancer dans l'écriture, d'abord pour le plaisir.
Tout d'abord, mon objectif était d'étendre les formalismes rencontrés en logique, en mathématiques ou en informatique pour les appliquer à des domaines totalement différents, notamment les arts, l'artisanat ou même les sports. Dans la même optique, je cherchais également à apporter des réponses à certaines questions inédites que je me posais parfois, et qui avaient pour caractéristique de mélanger différents champs : « Est-il possible d'écrire un roman avec la physique ? », ou encore « Est-il possible d'écrire un poème avec un langage informatique ? »1a.
C'est en explorant ces questions que j'ai été amené à vouloir dégager certaines opérations fondamentales de la pensée, mais aussi à interroger les concepts d'intelligence, de créativité, et de sens. Cette réflexion ne s'est pas limitée à un simple exercice théorique : elle est assortie de nombreux exemples pratiques, tirées de mes expériences personnelles, et propose également des techniques concrètes permettant d'aborder de nouveaux champs d'étude, tout en offrant des pistes pour générer de l'originalité.
Enfin, cette œuvre me permet de réunir en un même endroit des idées intéressantes provenant de disciplines variées, nourries par mes lectures et mes réflexions personnelles, tissant des liens entre elles. Elle s'inscrit ainsi dans une démarche philosophique plus large, poursuivant plusieurs objectifs : clarifier le langage et la pensée (épistémologie), intégrer différentes disciplines, et soulever des points liés à l'esthétique et même à l'éthique.
La difficulté d'un sujet aussi vaste et multidisciplinaire que celui de la pensée humaine réside d'une part dans l'impossibilité de développer toutes les spécialités qui s'y rattachent en quelques pages, et d'autre part dans l'incapacité d'en maîtriser toutes les facettes sans un engagement sur plusieurs vies d'études. Cette exhaustivité étant bien trop contraignante pour les idées que je cherche à transmettre, et dépassant de loin mes connaissances et la portée que je souhaite donner à ce texte, mes développements manqueront inévitablement de la rigueur propres aux sciences expérimentales. Par exemple, le formalisme que je propose, bien qu'ancré dans la réalité, demeure avant tout une construction intellectuelle. Il conviendrait donc de le confronter aux recherches scientifiques, pour voir dans quelle mesure celui-ci correspond à la manière dont le cerveau fonctionne.
L'autre défi réside dans la nature même du sujet, qui nous confronte aux limites du langage et, par extension, à nos propres limites cognitives. Parler du langage via le langage entraîne inévitablement une certaine confusion. Toutefois, cette tension entre ce que l'on veut exprimer et les moyens dont on dispose pour le faire constitue, à mon sens, une part de la beauté de cet essai : les concepts que je développe s'appliquent non seulement à la réflexion qu'ils tentent d'éclairer, mais aussi à ce même essai, qui devient une illustration vivante des idées qu'il propose. Il se fait ainsi écho, se répond, et se réajuste continuellement à lui-même, tout comme la pensée qui se nourrit de ses propres questionnements et évolue sans fin.
En fin de compte, j'ai essayé d'écrire l'œuvre que j'aurais voulu lire : un texte qui rassemble des questions existentielles intrigantes et qui interroge les fondements mêmes de la pensée et de la connaissance. Et tout cela avec un langage se voulant concis, clair et compréhensible, car je suis convaincu que la pensée devient véritablement fertile quand elle peut s'exprimer sans déguisement. Trop souvent, la philosophie et les sciences se perdent dans des méandres linguistiques ou des formalismes minutieux qui rendent des idées brillantes inutilisables, voire incompréhensibles. Pour ma part, je ne cherche pas à rendre ces concepts plus complexes qu'ils ne le sont, mais à les rendre accessibles et tangibles. Ce texte est un pont qui relie les idées au monde. Il ne prétend pas offrir des réponses définitives, mais est une invitation pour le lecteur à cheminer sur mes pas et à explorer ce qui anime notre pensée et notre compréhension du monde.
128. Voudrait-on poser des thèses en philosophie qu'on ne pourrait jamais les soumettre à la discussion, parce que tout le monde serait d'accord avec elles. L. Wittgenstein, Recherches philosophiques (1953)
Afin de construire un formalisme qui généralise la connaissance humaine de manière la plus large possible, j'aimerais pouvoir tenir compte de n'importe quelle perception possible, que j'appelerai un symbole. Ensuite, j'aimerais mettre en évidence une propriété importante de notre pensée qui est de pouvoir grouper des éléments ensemble.

Cet essai part d'un postulat simple : il y a des choses dans l'univers, plutôt que rien, et nous, êtres humains, sommes capables de percevoir certaines de ces choses, et même d'interagir avec.
Pour quelqu'un capable de lire ce texte, il me paraît difficile d'arguer le contraire, puisque lire ce texte implique de distinguer des caractères différents sur cette page, et a donc la capacité de percevoir différentes choses. La compréhension de ce texte présuppose la perception et même la cognition. Pour les objectifs que je poursuis dans cet essai, je me contenterai donc de cette proposition raisonnable au vu de notre expérience quotidienne de la vie2a, en ignorant les positions philosophiques extrêmes (e.g. qu'il n'y a rien, ou que l'être humain ne puisse rien connaître, etc.).
Étant donné que les mots « choses » ou « trucs » sont peu agréables à l'oreille (et sonnent peu sérieux !), j'utiliserai dans ce texte d'autres mots ayant une signification similaire comme « entités », « éléments », « informations » ou encore « symboles ».
Discussion Une première réflexion intéressante concerne le sens de ces mots, ou plutôt le constat de leur manque de sens. Par exemple, je n'utilise dans ce texte le mot information que comme un synonyme de quelque chose (plutôt que rien), que je ne définirai pas plus précisément. Par conséquent, lorsque je dis « Je perçois de l'infomation », je ne dis rien de plus trivial que « Je perçois quelque chose » (plutôt que rien). Son utilisation est pratique au vu de la connotation usuelle du mot information, qui est justement celle d'un mot fourre-tout, et du fait celui-ci puisse être utilisé aussi bien au singulier qu'au pluriel et même de manière indénombrable : une information, des informations, de l'information2b.
Discussion J'aimerais ici insister sur l'importance du choix d'un mot au vu de sa connotation usuelle, mais également sur la confusion qu'implique un tel choix par rapport à une définition physique ou ésotérique. Pour s'en rendre compte, il suffit de prendre d'autres exemples caricaturaux de mots habituellement détournés de leur acception physique pour être utilisés de manière vague : si j'avais nommé les choses de l'univers des énergies, cela aurait renvoyé à une autre connotation, alors même que j'aurais utilisé le mot exactement de la même manière dans ce texte. Pour être tout à fait neutre, il me faudrait utiliser un mot sans connotation aucune, par exemple un mot inventé comme « scrogneugneu »2c.
Discussion Dans Homo Deus (2015), Harari avance le concept de dataïsme pour exprimer le rôle prépondérant que joue l'information dans notre société, en référence aux médias, au “big data„, etc. et qu'il s'agit d'une sorte de nouvelle religion. Il est donc intéressant de remarquer que dans cette époque où le concept d'information joue un rôle aussi important, ce soit précisément cette notion qui serve de point de vue explicatif du monde. De la même manière qu'à l'époque de Descartes c'était la mécanique qui servait de point de vue explicatif du monde, ou dans la Grèce antique, la géométrie. On remarque là un pattern simple : nos modèles explicatifs sont fortement influencés par l'ère du temps (“zeitgeist„).
Notre perception est limitée. D'une part nos capteurs, c'est-à-dire nos sens, ont des résolutions, des portées et des sensibilités limitées, qui peuvent même varier dans le temps. Par conséquent, nous ne sommes capables de percevoir qu'une partie limitée d'information de notre environnement.
ExempleNos yeux ne peuvent détecter qu'un spectre restreint d'ondes électromagnétiques, le spectre visible. Nos oreilles ne sont sensibles à des sons que s'ils se situent dans un intervalle de fréquence donnée (environ 20Hz à 20kHz), et au sein de cet intervalle la sensibilité diffère en fonction de la fréquence. D'autres espèces vivantes sont quant à elles sensibles aux infrarouges, ultraviolets, infrasons ou ultrasons.
D'autre part, toutes nos perceptions résultent d'une intégration ou interprétation par notre organisme. En effet, nos perceptions dépendent de divers facteurs tels que nos sens, notre vécu, notre état physique et mental, le contexte dans lequel elles ont lieu, etc. Il en découle que toute perception est subjective.
Exemple Quelques exemples illustrant que toute perception résulte d'une intégration par notre organisme :
Anecdote Mon œil droit voit plus rouge que mon œil gauche qui lui voit plus vert. Je m'en rends compte lorsque je regarde une scène et ferme un de mes deux yeux.
❖
Dans cet essai je ne vais pas m'attarder plus que cela sur la manière dont la perception fonctionne biologiquement et physiquement, ni sur la nature ontologique et épistémologiques des entités que nous percevons (leur existence, leur réalité, la possibilité de les connaître « vraiment », etc.). Mon propos se situe donc au niveau de la perception telle qu'elle se manifeste, dans notre expérience quotidienne et concrète du monde2d.
Dans un même ordre d'idée, je resterai, sauf indication contraire, dans un cadre intra-cognitif : j'examinerai les opérations mentales qui peuvent se dérouler à l'intérieur d'un système cognitif isolé, sans aborder les différences d'interprétation entre individus ni les phénomènes collectifs liés au langage ou à la culture.
La capacité de perception en suppose une autre, celle de pouvoir distinguer des entités disparates, c'est-à-dire différencier certaines entités des autres parmi l'ensemble des informations perçues (« quelque chose parmi d'autres choses »). Cela nécessite le discernement de caractéristiques propres aux entités.
Exemple Je perçois le clavier d'ordinateur sur mon bureau comme une entité distincte de la table sur laquelle il se trouve. Je perçois la colère et la joie comme des émotions distinctes. Je perçois différents goûts dans un aliment, etc.

Cette capacité de distinction est essentielle : elle nous permet d'organiser notre expérience en unités reconnaissables, ce qui est une première étape fondamentale dans la construction de notre représentation du monde. Comme mentionné dans la section précédente, cette capacité perceptive et distinctive dépend de notre expérience, du contexte, et évolue avec eux.
Exemple Pouvoir distinguer différents cépages de vin lors d'une dégustation demande un apprentissage, une familiarisation progressive avec des distinctions de plus en plus fines.
Discussion La perception implique-t-elle nécessairement la distinction ? Ou peut-elle exister sans elle comme un « bloc brut » d'expérience indifférenciée ?
Par exemple, si j'ouvre les yeux dans un environnement uniformément blanc, sans aucune variation de lumière, de forme, de texture ou autre discontinuité, est-ce que je perçois quelque chose ? Si j'ai déjà connu l'expérience de la perception des couleurs, ou si je différencie ce blanc par rapport à la présence de mon corps, alors oui je perçois le blanc. Mais si je n'ai jamais vu d'autres nuances auparavant, et si je ne suis même pas capable de détacher mon corps de cet espace « blanc », ou de remarquer n'importe quel autre saillance dans cet espace, alors la notion de « blanc » s'effondre.
Il semble donc que le contraste (différence, variation, changement) soit un prérequis de la perception, et donc de l'apparition de la conscience. Si tout est identique sans aucune propriété notable, alors il n'y a rien à percevoir, donc rien dont puisse être conscient. Tout perception serait donc relative.
Discussion Cette relativité perceptive soulève des questions existentielles vertigineuses. Cela suggère, par exemple, que le positif dans nos vies (plaisir, beauté, joie, amour, etc.) n'est perceptible que par contraste avec le négatif (douleur, laideur, tristesse, perte, etc.). Il semble donc que le négatif soit structurellement nécessaire pour que le positif ait un sens, une intensité, une valeur. Se pose donc la question suivante : si l'on ne peut avoir l'un sans l'autre, le positif de nos vies vaut-il la peine que le négatif existe ?2e Ou, à l'inverse, vaut-il mieux renoncer à la perception du positif pour éviter le négatif ?2f
Le paradoxe c'est que nous, êtres humains, cherchons à maximiser le positif tout en tentant d'éradiquer le négatif. Entre les extrêmes théoriques, la solution pratique consiste-t-elle à réduire le négatif à une quantité minimale tolérée ?2g
Ayant souligné que toute perception est subjective, je vais maintenant définir le concept de symbole, qui constituera la brique de base de mon formalisme. Afin d'assurer sa généralité, j'adopte une définition délibérément large, capable d'englober toute perception humaine.
Définition J'appelle symbole toute expérience sensible.
Exemple Un signe graphique, un dessin, un stimulus visuel, un comportement, un son, une odeur, un mouvement, une sensation corporelle, une émotion, une pensée, etc.
Ici encore j'utilise à dessein le mot symbole au vu de sa connotation commune qui correspond assez bien au sens que je veux lui donner. C'est par ailleurs un mot courant en sémiotique2h.
Exemple Les lettres de l'alphabet ainsi que les chiffres sont des symboles. Les lettres minuscules sont des symboles différents des lettres majuscules de même que les chiffres arabes sont des symboles différents des chiffres romains, et ce bien qu'il existe des correspondances entre ces symboles. Deux symboles différents peuvent ainsi partager un même sens.
Grouper les « choses » constitue l'élément le plus profond, le plus indispensable de notre perception et de notre conception du réel. Watzlawick et al., Changements, paradoxes et psychothérapie (1975).
En plus de pouvoir distinguer différents symboles les uns des autres, une autre capacité primordiale consiste à considérer plusieurs entités comme formant un tout, ainsi que l'opération complémentaire qui consiste à décomposer un symbole en plusieurs sous-entités distinctes.
Exemple Je peux considérer quatre pieds ainsi qu'une planche en bois comme des entités séparées. Mais si elles sont judicieusement combinées, je peux les appréhender comme des parties formant un tout : une table. Réciproquement, je peux percevoir une table dans mon champ visuel, puis la décomposer mentalement en ses différents composants.
Définition J'appelle structuration l'opération consistant à considérer plusieurs entités distinctes comme formant un tout, et décomposition l'opération inverse consistant à considérer une entité comme étant composée de plusieurs entités distinctes, ses parties.

Idée Distinction, structuration et la décomposition me semblent être des opérations cognitives fondamentales. Peut-on établir une liste d'autres opérations cognitives de ce type ?
↑Les opérations complémentaires de structuration et de décomposition rendent possibles des relations d'ordre, ou hiérarchie, entre symboles.
Discussion En croisant ces notions, on peut imaginer des hiérarchies paradoxales dans lesquelles certains éléments se trouvent à la fois au même niveau et à des niveaux différents : un tout qui serait aussi une partie, et vice-versa.2i
Tout au long de cet essai, je devrai distinguer différents symboles et spécifier les relations qu'ils entretiennent. Pour faciliter l'identification des niveaux hiérarchiques, j'utiliserai les préfixes proto- et méta- :
Exemple Pour dire que plusieurs symboles combinés (les parties) forment un nouveau symbole (le tout) je dirai qu'ils forment un méta-symbole. Conversément, pour dire qu'un symbole (le tout) est décomposé en sous-symboles (les parties), je dirai qu'il est décomposé en proto-symboles.
Il est important de noter que les préfixes méta- et proto- sont toujours relatifs à un niveau hiérarchique de référence, que l'on choisit en fonction du contexte.
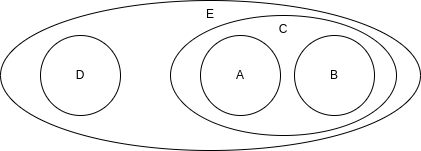
Par commodité, on peut numéroter les niveaux hiérarchiques pour mieux les distinguer, le début de la numérotation étant arbitraire2j.
Exemple Reprenant l'exemple précédent, si le symbole C est considéré comme étant au niveau 2, alors la numérotation s'établit ainsi :
| Niveau | Symboles |
|---|---|
| 1 | A, B |
| 2 | C, D |
| 3 | E |
Il est également possible de modifier ce niveau de référence. Si le symbole C est considéré comme étant au niveau 0, on obtient alors :
| Niveau | Symboles |
|---|---|
| -1 | A, B |
| 0 | C, D |
| 1 | E |
Dans la suite de cet ouvrage, je me référerai souvent à des combinaisons de symboles à partir d'une liste de départ. Pour alléger la terminologie, je vais introduire comme synonyme de méta-symbole le terme de structure.
Définition J'appelle structure une combinaison de plusieurs symboles, les parties formant un méta-symbole, le tout.
Exemple Prenant les lettres de l'alphabet comme symboles de départ, nous pouvons les combiner en une structure que nous appelons communément un mot. Le mot chat par exemple peut être vu comme une structure composée des symboles c, h, a et t.
Exemple Regardant des nuages dans le ciel, nous pouvons percevoir différents symboles parmi ceux-ci : des traits, des nuances de couleurs, etc. Parmi cet ensemble de symboles, notre cerveau est capable de distinguer des structures : visages, animaux, objets, scènes diverses, etc.
Discussion Dans le langage courant, le mot structure est utilisé de différentes manières. Pour la clarté de ce texte, il est important de distinguer ces différentes acceptions :
En effet, si l'on omet cette distinction, cela peut donner lieu à des phrases très confuses. Par exemple, si l'on considère qu'un ensemble de mots forme une structure appelée phrase, on pourrait poser la question suivante : « Quelle est la structure (forme) de cette structure (phrase) ? ». Pour éviter tout ambiguïté, je parlerai donc de la structure abstraite, ou forme d'une structure (concrète).
Exemple La phrase Le chat court derrière la souris peut être vue comme une structure (concrète) composée des symboles Le, chat, court, etc. La structure de abstraite, ou forme, de cette phrase pourrait être déterminant + nom + verbe + préposition + déterminant + nom.
De manière plus intuitive, il apparaît qu'une situation donnée ne peut jamais faire l'objet d'une description exhaustive et qu'une série de choix, explicites ou implicites, préside toujours à une démarche de description d'une situation donnée. {...} cela signifie que des choix sont posés qui distinguent les informations jugées pertinentes de celles qui ne le sont pas. B. Feltz, La science et le vivant (2014)
Les préfixes proto- et méta- peuvent également être appliqués au mot structure afin de décrire d'autres niveaux d'analyse où des structures peuvent elles-mêmes être des parties (proto-structures) ou des ensembles plus vastes (méta-structures).
Exemple Avec les lettres de l'alphabet comme symboles de départ, nous formons des structures appelées mots. Mais les mots eux-mêmes peuvent être combinés afin de former des phrases, qui sont des méta-structures. Les phrases peuvent à leur tour être assemblées afin de former des paragraphes, qui sont des méta-méta-structures, etc.
En se plaçant à différents niveaux hiérarchiques2k, on voit donc comment il est possible de créer des entités de plus en plus complexes ou de plus en plus simples :
J'appelle gigognité2l cette possibilité de pouvoir combiner récursivement des entités de plus en plus complexes et de pouvoir décomposer récursivement des entités de plus en plus simples.
Discussion Un symbole peut-il toujours être décomposé en proto-symboles ? À l'échelle de l'univers, cela revient à se demander s'il existe des unités indivisibles d'information, si l'univers est discret ou bien continu. Question qui est du ressort de la physique.
Il n'y a donc pas de différence absolue entre la notion de symbole et la notion de structure, seulement une différence relative à un niveau d'analyse donné2m. Je dois d'abord définir ce que je considère comme étant un symbole, pour savoir ce que je considère comme étant une structure. Ou bien, à l'inverse, je définis d'abord ce que je considère comme une structure, afin de déterminer ce que je prends pour un symbole.
Exemple Le signe ci-dessous peut être considéré comme étant « un » symbole, c'est-à-dire comme étant un tout indivisible, ce qui correspond bien à l'usage courant que l'on peut faire du mot symbole. Mais on peut aussi l'envisager comme une structure, composée d'éléments visuels distincts: un cercle, une ligne ondulée et deux points. À un niveau d'analyse plus fin, la ligne ondulée peut elle-même être vue comme une structure formée de deux sinusoïdes.

C'est donc l'interprétation de l'observateur qui détermine ce qu'il considère comme un symbole, c'est-à-dire un élément qu'il n'approfondit pas davantage, et ce qu'il considère comme une structure, c'est-à-dire un ensemble qu'il décompose en parties. Le niveau de précision sera choisi en fonction des objectifs pratiques d'analyse, de perception ou de modélisation que l'on souhaite atteindre.
Exemple Reprenons l'exemple d'un mot formé d'un ensemble de lettres, où les lettres sont considérées comme des symboles, et le mot comme une structure.
En plus de la subjectivité du choix du niveau d'analyse, il n'existe en général aucune unicité dans le nombre de niveaux hiérarchiques que l'on peut choisir pour décomposer une structure ou combiner des symboles donnés. Autrement dit, pour une même entité perçue, plusieurs découpages hiérarchiques sont possibles.
Exemple Une première manière d'aborder la phrase Le chat court derrière la souris et de la considérer comme une structure composée directement des symboles Le, chat, court, derrière, la, souris. Cela correspond à une modélisation à deux niveaux hiérarchiques.
Mais on peut aussi introduire un niveau intermédiaire avec deux proto-structures, Le chat court (proposition principale) et derrière la souris (groupe prépositionnel), chacune composée de mots. Nous avons alors trois niveaux hiérarchiques.
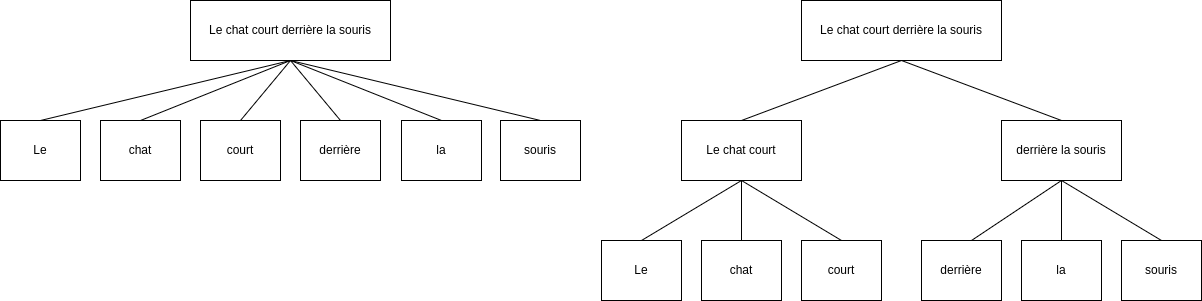
La hiérarchie entre symboles et structures n'est donc ni objective ni unique, mais dépend du choix de niveau de granularité.
65. [...] Au lieu d'indiquer un trait commun à toutes les choses que nous appelons langage, je dis que ces phénomènes n'ont rien de commun qui justifie que nous employons le même mot pour tous, — mais qu'ils sont tous apparentés les uns aux autres de bien des façons différentes. 71. On peut dire que le concept de "jeu" est un concept aux contours flous. — « Mais un concept flou est-il vraiment un concept ? » L. Wittgenstein, Recherches philosophiques (1953)
Je retrouve chez Karl Popper2n l'idée selon laquelle une théorie qui n'est pas falsifiable est une théorie inutile. Or les concepts de symbole et de structure tels que je les ai définis sont tellement généraux qu'on peut se poser la question de leur pertinence.
En effet, le concept de symbole faisant référence à toute expérience sensible, il n'existe, par définition, rien qui ne puisse être considéré comme un symbole. Il est donc, par construction, infalsifiable. D'autre part, je n'ai pas précisé ce que j'entendais par combinaison de symboles dans ma définition d'une structure, ce qui laisse ouvertes toutes les interprétations.
Un autre inconvénient réside dans le fait qu'en regroupant des concepts disparates sous un même vocable, on risque de perdre de vue leurs différences fondamentales. Il n'est peut-être pas pertinent, voire possible, de regrouper de manière aussi large des phénomènes aussi variés.
En revanche, l'avantage d'avoir des définitions aussi évasives, c'est que cela permet de les adapter à n'importe quelle situation. C'est en précisant ce que l'on entend par symbole et combinaison que l'on circonscrit le type de structure considéré.
Discussion Ce constat amène à une réflexion sur le langage : moins un terme est défini et plus il possède un potentiel polysémique, c'est-à-dire la capacité de signifier plusieurs choses différentes. Un mot vague est en quelque sorte un conteneur dynamique pouvant accueillir divers sens en fonction du contexte. À l'inverse, un mot strictement défini perd cette capacité, car il n'est plus possible de lui attribuer un autre sens.
Discussion Cette observation linguistique me conduit à une analogie issue d'un autre domaine. En théorie de l'information, il y a une définition de la quantité d'information (ou entropie) que j'ai toujours trouvée terriblement contre-intuitive : plus un message est incertain et plus il contient d'information, tandis qu'un message certain (prédictible) ne contient aucune information (nouvelle).
Exemple Si deux personnes communiquent et que la première répète toujours la même phrase, la seconde n'apprend rien de nouveau à chaque fois car le message est parfaitement prévisible.
De manière analogue, un terme flou, riche en possibilités sémantiques, peut être vu comme porteur d'une entropie élevée. Tandis qu'un terme strictement défini a une entropie faible.
Discussion Enfin, on peut également appliquer ces considérations au déroulement d'une conversation. Lorsqu'un interlocuteur parle, les possibilités que je sois surpris sont plus grandes, car il n'est pas possible de prédire exactement ce qu'il va dire. En revanche, lorsque c'est moi qui prend la parole, étant donné que je contrôle ce que je dis, c'est comme si je figeai le réel. Une autre illustration de ce phénomène est celle de la rencontre avec une personne inconnue. Tant que l'on n'a pas eu l'occasion de discuter avec elle, sa personnalité, son histoire sont pleines de potentialités. Mais plus les interactions se multiplient, plus ces possibles se réduisent, car on en apprend davantage sur cette personne et on finit par en saisir les contours. Une autre métaphore est celle du peintre face à une toile blanche : tant que le cadre reste blanc, l'œuvre est pleine de potentialités. Mais dès que le peintre pose un coup de peinture, cela limite le nombre de possibilités restantes, car chaque geste définit une direction, une forme, une couleur, et exclut d'autres alternatives. À partir de ce moment, la toile commence à prendre une forme précise, et chaque nouveau coup de pinceau réduit l'espace des choix à venir, jusqu'à ce que l'œuvre soit complète et figée.
Ce qui est en tout cas certain, c'est qu'il y a un signe qui, s'il ne peut se substituer à tous les chevaux, vaut au moins pour quelque chose que, par commodité, nous nommerons l'idée de cheval. Umberto Eco, Le Signe (1980)
Ayant établi les bases de cet essai, il reste à explorer d'autres opérations fondamentales de la pensée : la capacité de faire référence à des objets à travers un nom ou un symbole, ainsi que la possibilité d'envisager des alternatives entre différents symboles. Ces deux mécanismes, à la fois cognitifs et structurels, annoncent une forme d'abstraction, de reconnaissance de patterns ainsi que de compression de l'information. Une fois ces notions clarifiées, nous pourrons alors aborder le concept de langage.
En préambule aux idées développées dans ce chapitre, je vous propose un exemple pratique appliqué à la mixologie, qui est l'art de mélanger des ingrédients pour créer des cocktails. Par ailleurs, cette section permettra de cimenter les notions de symbole et structure abordées précédemment.
Anecdote Si j'illustre ce chapitre par des exemples issus de la mixologie, ce n'est pas pour inciter le lecteur à la consommation d'alcool, mais parce qu'il s'agit d'un des domaines dans lequel j'ai, pour la première fois, expérimenté un formalisme abstrait inspiré de la forme de Backus-Naur. J'avais en effet remarqué que de nombreux cocktails partageaient des patterns communs et cherchais un moyen simple de les mémoriser. Par coïncidence, je relisais à ce moment-là un ouvrage de programmation mentionnant cette notation3a, que j'ai trouvée étonamment adaptée à mon besoin.
Un des premiers patterns que j'ai remarqué est que les cocktails les plus simples résultent du mélange d'un soft-drink, c'est-à-dire une boisson non alcoolisée (abr. soft) avec un alcool. Je l'écris via la notation suivante :
cocktail : soft + alcool
Cette notation peut se traduire par « un cocktail est une structure formée par la combinaison des symboles soft et alcool ».
Cependant « soft-drink » et « alcool » représentent des notions abstraites. Il s'agit de termes génériques qui peuvent faire référence à différentes boissons. Voici une définition possible de la catégorie soft :
soft : eau | jus d'orange | jus de citron | cola | tonic
Cet encadré peut se lire « un soft, c'est soit de l'eau, soit du jus d'orange, soit du jus de citron, soit du cola, soit du tonic ». Et nous pouvons définir de la même manière ce qu'est un alcool :
alcool : rhum | whisky | vodka | gin | tequila
En assemblant les trois définitions précédentes, nous nous retrouvons alors avec le système suivant :
soft : eau | jus d'orange | jus de citron | cola | tonic alcool : rhum | whisky | vodka | gin | tequila cocktail : soft + alcool
Remarquons la hiérarchie existante entre ces définitions : cocktail est une définition d'un niveau supérieur à soft et alcool. Notons également la différence de précision entre ces symboles : les symboles soft et alcool sont plus abstraits relativement aux symboles eau, jus d'orange, rhym, whisky, etc. qui eux sont plus concrets. La définition de cocktail se situe donc à un niveau d'abstraction supérieur.
Il est toutefois possible de passer d'un symbole général à un symbole plus particulier en l'instanciant. Cela consiste pour chaque abstraction présente dans la définition de cocktail à choisir une des alternatives possibles.
Parmi toutes les possibilités qu'offre mon système, je décide ainsi d'utiliser comme soft du jus d'orange, et comme alcool de la vodka :
soft => jus d'orange alcool => vodka cocktail : soft + alcool
Ce qui me permet finalement d'instancier cocktail en une structure concrète :
cocktail => jus d'orange + vodka
Et de lui attribuer son nom consacré :
screwdriver : jus d'orange + vodka
Dans notre quotidien, nous utilisons constamment des mots pour désigner des choses : des objets, des êtres, des émotions, des idées, des concepts, etc.
Exemple Le mot chaise désigne un objet fonctionnel précis, toute comme le mot cheval renvoie à un animal avec certaines caractéristiques, le mot joie à un certain état mental et physique, le mot triangulaire à une forme déterminée, le mot totalitarisme à un type de société, le mot paradis à un concept imaginaire, etc.
Cognitivement, nous avons donc non seulement la capacité de considérer qu'un ensemble d'éléments forme un tout, mais nous pouvons également associer à ce tout un symbole, qui n'est pas nécessairement un nom, pour le représenter. Cela correspond à l'usage courant du mot symbole.
Exemple Le drapeau d'un pays fait référence à ce pays. En reconnaissant ses couleurs et ses formes, de nombreux éléments nous viennent spontanément à l'esprit : sa cuisine, ses paysages, son histoire, ses villes, etc. Le symbole du drapeau active ainsi un réseau de symboles associés, dont chacun peut à son tour en activer d'autres. Nous en reparlerons lorsque nous aborderons la sémantique des symboles.
Par conséquent, pour faire référence à une structure, plutôt que d'en représenter explicitement les éléments à chaque fois, je peux utiliser un symbole déterminé. J'établis pour cela une correspondance entre la structure et un symbole, une convention linguistique ou cognitive qu'un symbole donné évoquera une structure particulière. Cette capacité de symbolisation, « établir un lien entre une chose et une autre chose », me semble être une autre opération fondamentale de la pensée.
Définition J'appelle définition, ou symbolisation, la correspondance établie entre une structure et un symbole qui la désigne.
Exemple Pour faire référence à un mélange de vodka et de jus d'orange, plutôt que de répéter constamment l'expression « vodka jus d'orange », je peux utiliser le nom consacré qui désigne cette structure, « screwdriver ».

Nous avons ainsi défini ce qu'est un screwdriver, ou en lisant de droite à gauche, symbolisé un vodka jus d'orange.
Analogie De la même manière qu'en informatique une variable « pointe » vers une valeur en mémoire, une définition peut être vue comme un symbole qui « pointe » vers un autre symbole.
Méta Remarquons au passage que ma définition d'une définition s'applique aussi aux définitions de cet essai :

Notation Jusqu'à présent j'ai utilisé des diagrammes afin d'illustrer certains points concernant les symboles et les structures. Désormais, j'introduirai un autre formalisme, inspiré de la forme de Backus-Naur3b (abr. BNF), afin de clarifier mes exemples :
screwdriver : vodka + jus d'orange
Cet exemple se lit : « Un screwdriver est une combinaison de vodka et de jus d'orange ».
: » indique une définition : le symbole à sa gauche (definiendum) renvoie à la structure à sa droite (definiens).
+ » indique une combinaison de symboles, et donc l'opération de structuration.
Les propriétés de relativité et de hiérarchie que nous avions observées à propos des symboles et des structures s'appliquent également dans le cas des définitions.
Dans ma définition d'une définition, on ne se formalisera donc pas sur la distinction entre une structure et un symbole : ce peut aussi bien être la correspondance entre un symbole et une structure, qu'entre deux symboles ou deux structures.
Exemple Dans un jeu de société, un cube brun peut représenter une ressource particulière, comme du bois. Tandis qu'un cube gris peut symboliser un autre matériau, comme de la pierre, et un meeple brun peut représenter un joueur. C'est donc bien la combinaison de deux symboles, cube et brun, et la structure résultante qui symbolise du bois.
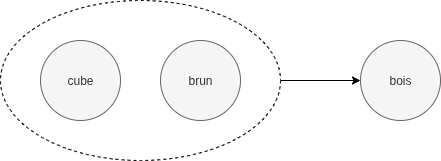
cube + brun : bois
Discussion Les plus perspicaces se demanderont peut-être si la notation « cube + brun : bois » est équivalente à la notation « bois : cube + brun » ? Nous verrons plus loin que, selon le contexte, l'un ou l'autre sens peut être privilégié, ou même que la distinction peut être ignorée.
Exemple Voici un autre exemple où un symbole référence un « seul » autre symbole plutôt qu'un ensemble de symboles :

brasier : incendie
Dans mon exemple précédent où brasier pointe vers un incendie, il est intéressant de garder à l'esprit qu'incendie n'est un symbole qu'en vertu du niveau d'analyse adopté : il représente en fait une structure implicite, le condensé d'une structure plus large que l'on pourrait développer si nécessaire.
incendie : flammes + fumée + chaleur brasier : incendie
À partir d'une définition donnée, il est ainsi possible de développer des méta-définitions, ou des proto-définitions, créant un système hiérarchique de définitions.
Exemple L'exemple suivant illustre des mélanges de couleurs :
vert : jaune + bleu orange : jaune + rouge brun : vert + orange
jaune, bleu et rouge forment le niveau hiérarchique le plus bas (niveau 1). Ce sont des symboles élémentaires non explicitement définis3c.vert et orange constituent un niveau hiérarchique intermédiaire (niveau 2), car chacun est défini à partir de symboles de niveau 1.brun correspond au niveau hiérarchique le plus élevé (niveau 3).Méta Enfin, on peut également considérer l'ensemble de la définition comme étant un tout et l'utiliser comme n'importe quel autre structure, ou symbole.
Exemple La définition « vert : jaune + bleu » peut elle-même être vue comme une structure composée des symboles vert, :, jaune, + et bleu.
Remarquons qu'ici c'est bien l'ensemble de la définition « vert : jaune + blue » qui est englobée. Comme exemple de méta-structure, nous pouvons imaginer un « dictionnaire » de couleurs, dans lequel on collecterait cette définition ainsi que les autres :
dictionnaire : (vert : jaune + bleu) + (orange : jaune + rouge) + (brun : vert + orange)
Dans cette notation, chaque définition est traitée comme un symbole élementaire. Le dictionnaire devient ainsi une structure de niveau supérieur, regroupant toutes les définitions.
Cette approche illustre l'intérêt de l'universalité des concepts de symbole et de structure qui permet de construire des systèmes hiérarchiques et réflexifs, où tout objet peut à son tour servir de composant pour des structures plus complexes.
À partir de cette notion très générale de ce qu'est une définition, nous allons pouvoir en distinguer différentes formes en fonction des usages que nous en faisons.
Jusqu'à présent, nous avons abordé la définition comme désignant une structure concrète. Par exemple, si je vais dans un bar et demande un screwdriver, je m'attends à recevoir un mélange de vodka et de jus d'orange, c'est-à-dire l'ensemble de la structure à laquelle le mot screwdriver fait référence. Cela correspond à une définition intensive, qui décrit ce qu'est une chose par ses propriétés constitutives jointes.
Cependant dans notre vie quotidienne, nous sommes capables de faire un usage bien plus abstrait des symboles : certains mots, plutôt que de représenter une structure concrète, semblent plutôt représenter une catégorie de choses. Je peux ainsi définir alcool non pas comme un ensemble de propriétés, mais en énumérant les symboles qui appartiennent à cette classe de symboles :
alcool : rhum + whisky + vodka + gin + tequila
Cela correspond à une définition extensive, qui décrit ce qu'est une chose en énumérant différents éléments séparés qui lui appartiennent. Le symbole alcool pointe toujours vers une structure, cependant la manière dont nous l'utilisons diffère d'une définition intensive. Par exemple, si dans le même bar je demande un alcool, sans préciser lequel, je ne m'attends pas à recevoir un mélange de tous les liquides désignés par cette appellation, mais bien un seul d'entre eux. On peut donc envisager une définition extensive comme représentant une alternative entre différents symboles.
DéfinitionJ'appelle classification, ou catégorisation, la correspondance établie entre un symbole et un ensemble d'alternatives symboliques qu'il représente.
Notation Afin de bien distinguer ce type de définition, j'introduis la notation suivante :
alcool : rhum | whisky | vodka | gin | tequila
Celle-ci se lit « un alcool, c'est soit du rhum, soit du whisky, soit de la vodka, soit du gin, soit de la tequila ».
| » représente ici une alternative, ou le « ou » exclusif de la disjonction (vel). 3dLa classification peut être vue comme un passage du particulier au général. Mais l'opération inverse, le passage du général au particulier est également possible3e.
Définition J'appelle instanciation le fait d'assigner à une classe générale un des symboles particulier qu'elle représente3f.
Exemple À partir d'une classe générale comme alcool, nous pouvons instancier un symbole particulier, comme gin. Je le note de la manière suivante :
alcool => gin
Nous verrons plus loin que cette réversibilité entre particulier et général permet une dynamique essentielle : la navigation cognitive entre niveaux d'abstraction.
Discussion On notera qu'une instanciation n'a de sens que relativement à une classification préalablement définie. Comme souvent, c'est le contexte et les choix opérés qui détermineront s'il est pertinent ou non de distinguer entre différents vocables.
+ » représenterait donc la conjonction logique, « et ». ↩3e. En épistémologie le passage du général au particulier est appelé déduction, tandis que celui du particulier au général est appelé induction. ↩3f. Analogie Les notions de classe et d'instance sont inspirées par la programmation orientée-objet. ↩
La définition, qu'elle soit intensive ou extensive, remplit une fonction cognitive essentielle : elle permet de faire abstraction des détails de la structure considérée. Un symbole qui fait référence à autre chose peut ainsi être vu comme un contenant qui dissimule une partie de son contenu, mais qui en contrepartie permet de le manipuler plus aisément. Il s'agit d'un procédé qui est à la base de nombreux processus de nos vies, et notamment de toute forme d'organisation.
Exemple Le fait de mettre plusieurs feuilles (contenu) dans un dossier (contenant) permet de manipuler l'ensemble sans se soucier de chaque page prise isolément. On n'a plus à déplacer chaque feuille séparément : il suffit de déplacer le dossier tout entier. On réalise une économie cognitive en interagissant avec la structure, et en faisant abstraction de la diversité et du nombre de symboles la composant.
Toutefois, le substitut symbolique utilisé n'est pas totalement équivalent à la structure qu'elle représente : il implique nécessairement une perte d'information.
Exemple Pour désigner à mon interlocuteur un « cheval », plutôt que de devoir avoir un cheval physiquement présent aux alentours, je peux lui montrer une photographie, un simplement, ou simplement le mot « cheval ». Mais en utilisant un symbole substitutif, la richesse des sensations qu'impliquerait la présence d'un véritable animal, son odeur, son comportement, ses sons, son allure, s'est évaporée.
Cette perte d'information a pour conséquence que plus un symbole se substitue à une expérience directe, plus il devient général et éloigné des choses qu'il représente.
Exemple Le symbole fruit nous paraît plus abstrait que le symbole pomme, parce que pomme représente quelque chose de plus précis, dont une avons une image mentale plus individualisée. Il s'agit d'un mot qui circonscrit plus étroitement le réel.
Il semble ici que le monde physique, notre réalité sensorielle, quoi qu'imparfaite, serve de critère afin de tracer cette frontière entre le concret et l'abstrait.
Définition J'appelle abstraction le degré selon lequel un symbole s'éloigne, relativement à un autre, de la réalité sensorielle qu'il représente.
Partant de cette définition, nous aimerions pouvoir établir une sorte de hiérarchie de l'abstraction3g : l'expression une pomme est plus concrète que un fruit, elle-même plus concrète qu'un aliment, ou encore une chose. Mais cette hiérarchisation entraîne rapidement des difficultés3h :
Il me paraît donc plus prudent d'envisager l'abstraction, non pas comme un absolu, mais comme une relation contextuelle entre symboles.
Exemple Dans un manuel de botanique, fruit pourra être un terme précis (opposé à feuille ou racine), tandis que dans un contexte culinaire, il deviendra une catégorie très large.
Nous en revenons finalement à deux idées développées dans le chapitre précédent. Tout d'abord qu'une situation donnée ne peut jamais faire l'objet d'une description exhaustive. Et ensuite que c'est notre décision subjective qui détermine le niveau de détail. La distinction entre abstrait et concret relève d'un choix, qui n'est pas forcément arbitraire, mais nécessairement singulier.
Discussion L'usage le plus concret que l'on pourrait faire d'une définition serait probablement d'attribuer un symbole pour chaque pomme particulière, un peu à la manière dont nous attribuons des noms aux personnes. L'expression cette pomme désigne en effet une structure bien délimitée dans la réalité.
Cependant l'expression cette pomme représente aussi une forme de généralisation à hauteur de mon ignorance : quelle est sa concentration en sucre ? L'épaisseur de sa peau ? Le nombre de ses graines ? Tant que je ne le sais pas, c'est comme si cette pomme valait pour toutes les configurations alternatives possibles3i.
On notera donc qu'un concept plus particulier n'est pas nécessairement moins abstrait : décrire la composition chimique d'une pomme, c'est être plus précis, mais c'est aussi s'éloigner du niveau perceptif auquel nous faisons quotidiennement référence.
En général, une classification n'est pas qu'un simple regroupement aléatoire de symboles, mais réuni des symboles ayant certaines propriétés en commun.
Exemple La propriété commune aux symboles regroupés dans la classe alcool est de contenir de l'éthanol.
Définition J'appelle pattern3j un symbole commun observé entre différentes structures.
L'idée de pattern renvoie donc à la notion de répétition : un motif, une caractéristique partagée par différents éléments.
Méta Au cours de cet essai, nous avons déjà rencontré plusieurs formes de dualité : partie/tout, particulier/général, concret/abstrait. Ces trois concepts sont unis par un pattern récurrent : celui de l'opposition entre deux notions.
Cette identification de régularités prend toute son ampleur lorsqu'elle concerne des structures appartenant à des domaines différents et des contextes variés. Elle permet alors d'établir des analogies et de créer des liens inédits entre des systèmes ou des idées a priori disparates.
Exemple En observant les pieds de maïs, on remarque que de nombreuses racines partent de la tige centrale, se ramifiant dans toutes les directions. Avec de l'imagination, on peut remarquer que ceux-ci évoquent visuellement les pattes d'une tarentule. La reconnaissance de ce pattern crée ainsi un lien entre deux entités très différentes, en mettant en lumière une organisation similaire.


Discussion Cette vision des patterns comme reconnaissance de symboles, de structures est inspirée du machine learning en intelligence artificielle. Prenons l'exemple d'un programme informatique entraîné à reconnaître des photographies de chats. Nous commençons à présenter une série d'entraînement au script, qui va apprendre à identifier certaines patterns spécifiques à l'apparence des chats : leur forme, leur taille, leur posture, etc.. Face à une nouvelle image, qui n'appartient pas à la série initiale, le programme sera alors capable déterminer s'il s'agit d'un chat en se basant sur les motifs qu'il a appris à reconnaître.


Mais l'aspect le plus fascinant de cette approche, qu'est qu'on peut aller au-delà de la simple reconnaissance : on peut présenter l'image d'un chien au programme, qui quantifiera alors la probabilité que cette image soit d'un celle chat. Autrement dit, nous pouvons donner un sens à la question « À quel point ce chien est-il un chat ? », comme étant celui de savoir à quel point un chien est similaire visuellement à un chat.

Cette capacité à quantifier la ressemblance entre des objets qui ne sont pas identiques ouvre des perspectives étonnantes. En répétant l'opération avec toutes sortes d'images, on peut conduire le système à résoudre des problèmes du type, « À quel point ce véhicule est-il un chat ? », « À quel point ce paysage est-il un chat ? » ou encore « À quel point cette peinture abstraite est-elle un chat ? ». De telles questions, qui semblent absurdes au premier abord, prennent tout leur sens lorsqu'on les interprète comme une interrogation sur la manière dont les structures visuelles de ces objets peuvent correspondre à celles observées chez un chat, comme un processus de comparaison entre patterns.
Anecdote Lorsque j'ai commencé à rédiger cet essai en 2019, l'IA générative était encore relativement inconnue du grand public, ce qui rendait l'illustration de concepts comme celui-ci moins intuitive. Aujourd'hui que celle-ci fait partie de notre quotidien, nous ne nous étonnons plus lorsque ces systèmes font des associations surprenantes, « hallucinent » des liens inattendus, ou génèrent des images remplies de patterns similaires. Je constate que cette évolution rend mon propos bien plus palpable.
L'un des effets pratiques de la définition et de la classification, et plus largement de toute structuration, est de conduire à une compression de l'information. En effet, la définition d'un concept permet de réduire la quantité d'information nécessaire pour le représenter, tandis que la catégorisation permet d'éliminer des détails spécifiques pour ne conserver que certaines caractéristiques communes.
La reconnaissance de patterns joue un rôle clé dans cette compression de l'information. En identifiant des régularités, des répétitions ou des structures similaires, il est possible de condenser un ensemble d'informations en une forme plus simple.
Exemple La structure binaire 101101101101101 peut être condensée si l'on remarque qu'elle est composée de cinq répétitions successives du motif 101. Il devient possible de la représenter de manière plus compacte en indiquant simplement cette répétition, plutôt que la chaîne entière, par exemple via la notation 101*5.
Ce principe sous-tend d'ailleurs les algorithmes de compression utilisés en informatique pour réduire la taille des données tout en préservant leur intégrité.
Exemple Le texte suivant contient 166 caractères, espaces comprises :
Un processus de communication dans lequel il n'existe pas de Code, et dans lequel il n'existe donc pas de signification, se réduit à un processus de stimulus-réponse.
Il est possible de le compresser en remplaçant certains mots, ou groupes de mots répétitifs, par un signe équivalent. Dans cet exemple, nous remarquons qu'une chaîne assez longue, dans lequel il n'existe
, se répète deux fois. Nous pourrions donc la coder, c'est-à-dire la remplacer par un signe équivalent. En adjoignant la règle de déchiffrage au message pour qu'il puisse être décodé, nous nous retrouvons ici avec seulement 150 caractères, soit un gain de 16 caractères :
# : dans lequel il n'existe Un processus de communication # pas de Code, et # donc pas de signification, se réduit à un processus de stimulus-réponse.
Plus la structure présente de répétitions ou de régularités, et plus le potentiel de compression est élevé3k. Pour gagner encore quelques caractères, nous pourrions également coder le mot processus
, et ainsi de suite :
# : dans lequel il n'existe % : processus Un % de communication # pas de Code, et # donc pas de signification, se réduit à un % de stimulus-réponse.
❖
Dans l'exemple précédent, le message contient la règle qui permet de le décompresser. Il s'agit donc d'une compression sans perte, qui permet de restituer exactement le contenu d'origine. À l'inverse, une compression avec perte sacrifie une partie de l'information afin d'obtenir une représentation plus compacte. Elle repose sur une forme de sélection perceptive : seules les composantes jugées pertinentes pour un certain usage ou contexte sont maintenues.
Ce principe se retrouve à la fois dans les algorithmes informatiques et dans le système cognitif humain, tous deux cherchant à compresser l'information pour en faciliter le traitement. Nos représentations mentales tendent ainsi à condenser la complexité du monde perçu, tout comme notre mémoire simplifie nos expériences, pour n'en revenir que certains traits saillants.
Dans mon exemple introductif, l'utilisation d'une définition abstraite comme « cocktail : soft + alcool » représente une compression d'information qui me permet de mémoriser plus facilement des recettes de cocktails3l. Plutôt que de retenir chaque recette, le fait de connaître un pattern me permet ensuite de reconstituer les recettes qui y correspondent, de décompresser l'information :
jus d'orange + vodka jus de citron + rhum cola + rhum cola + whisky tonic + gin
Discussion Anticipant sur la question de la signification, notons que c'est cette compression symbolique qui rend la communication possible, mais aussi incertaine car chaque interlocuteur doit décompresser le message reçu en rétablissant les significations implicites. D'où l'enjeu de toute transmission de sens : jusqu'à quel point mon interlocuteur est-il capable de restaurer l'information qui a été compressée via l'usage du langage ?
se mémorisait moins bien qu'une série d'exemples particuliers que l'élève généralisait ensuite de lui-même. ↩
Une grammaire est un ensemble de règles qui définit comment construire des « phrases » à partir des « mots ». [...] Tout ensemble de mots s'appelle un langage formel. P. Van Roy & S. Haridi, Programmation : Concepts, techniques et modèles (2007)
Nous disposons désormais de tous les composants nécessaires pour parler d'un langage proprement dit : un système de règles qui détermine comment ces symboles peuvent se combiner pour engendrer des structures.

Dans son acception courante, la notion de langage se réfère généralement aux langues naturelles comme le français. Dans cet essai, j'aspire à utiliser la notion de langage dans un sens beaucoup plus large. On pourra être familier des expressions « langage de programmation », ou encore « langage formel » pour désigner la logique ou les mathématiques. Mais je souhaite également y inclure des domaines comme l'architecture, le cinéma, la danse, la mode, la musique, la peinture, le sport, la cuisine, etc., que l'on peut eux aussi envisager comme des langages.
Un langage est généralement défini comme étant constitué d'une syntaxe, l'ensemble des règles régissant la formation des phrases, et d'une sémantique, qui s'intéresse à ce que les signes du langage désignent « dans le monde réel ». Dans ce chapitre, nous allons nous concentrer sur la syntaxe : celle-ci comprend un alphabet, c'est-à-dire les différents signes pouvant être utilisés, ainsi qu'une grammaire, c'est-à-dire des règles établissant la manière dont les signes peuvent être combinés.
Exemple Les lettres de l'alphabet constituent l'alphabet de la langue française. La constitution des mots est régie par une grammaire, plus précisément des règles phonotactiques ou morphologiques, de sorte que certaines combinaisons de lettres sont courantes (des syllabes comme ba/be/bi/bo/bu, ma/me/mi/mo/mu, pa/pe/pi/po/pu, ra/re/ri/ro/ru, etc.) mais d'autres n'apparaissent jamais (des séquences comme « oii », « aei », « np », « dl », « lx », etc.).
Définition J'appelle langage un ensemble défini de symboles, associé à un ensemble de règles de combinaison4a.
Dans cette définition, l'ensemble déterminé de symboles correspond donc à la notion d'alphabet, et les règles de combinaison à la notion de grammaire. À partir de cette syntaxe, il est possible de former diverses structures.
Exemple Je définis un langage très simple dont l'alphabet ne contient que deux symboles, 0 et 1. Comme règle de combinaison, je spécifie que trois symboles doivent être juxtaposés les uns à côté des autres. Avec ce langage basique, il est possible de former 8 structures distinctes : 000, 001, 010, 100, 011, 101, 110, 111.
Nous pourrions décrire ce langage avec la notation BNF :
symbole : 0 | 1 structure : symbole*3
Qui se lirait alors :
symbole c'est soit 0, soit 1.
structure est formée par la combinaison de trois symboles. le symbole astérisque « * » a la même signification qu'une multiplication en mathématiques : il s'agit de sucre syntaxique pour exprimer plusieurs additions. En l'occurrence nous aurions pu écrire « structure : symbole + symbole + symbole » à la place de « structure : symbole*3 ».
❖
Un langage tel que défini ici, est donc simplement un choix de système de définitions, une délimitation de symboles et de structures.
Discussion Dans la littérature spécialisée, ce sont souvent les termes de la langue naturelle qui sont repris comme termes génériques : alphabet et grammaire permettent de former des mots. On parle par exemple d'un « mot binaire » de trois chiffres pour désigner la séquence 110. Je trouve cependant que ces termes évoquent trop les langues parlées, et entraîne donc une confusion (« Les lettres de l'alphabet constituent l'alphabet de la langue française »). C'est pourquoi je leur préfère les termes plus neutres de symboles, règles de combinaison et structures.
Discussion J'ai démarré cet essai en abordant la notion de structure comme résultant de nos perceptions. Avec la notion de langage, j'aborde plutôt la notion de structure comme une construction artificielle ou formelle. Bien que ces approches s'interpénètrent, nous pouvons les distinguer conceptuellement :
Un alphabet de symboles équipé de règles de combinaison définit un ensemble de structures « potentielles ». Cet espace, au sens mathématique du terme, de structures est constitué de l'ensemble des combinaisons possibles de symboles via les règles données.
Exemple Reprenons l'exemple simple du langage aux symboles de base 0 et 1 et dont la règle de combinaison consiste à juxtaposer trois symboles. Ce langage rend possible la construction de 23 = 8 structures, qui sont l'ensemble des mots binaires à trois chiffres.
Il convient de distinguer langage permettant de créer un ensemble fini de structures, d'un langage permettant d'en créer théoriquement une infinité. Dans le premier cas, il sera en effet possible de dénombrer le nombre de structures définies par le langage mais pas dans le second cas.
Exemple Prenons pour ensemble de départ les 26 lettres de l'alphabet. Spécifions comme règle de combinaison que plusieurs lettres peuvent être juxtaposées les unes à côté des autres. Voici une notation permettant de définir ce langage, où l'astérisque désigne la combinaison d'un nombre quelconque de symboles4b :
lettre : a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z mot : lettre*
Dans cet exemple, comme il est possible de juxtaposer un nombre quelconque de lettres, le nombre de structure potentielles autorisées par ce langage est infini. Pour pouvoir les dénombrer, il faut donc se limiter à un niveau donné. Par exemple, il y a 262 = 676 mots comportant deux lettres, 263 = 17576 mots comportant trois lettres, et en généralisant, 26n mots à n lettres. ❖
Le dénombrement mathématique apparaît donc comme un outil privilégié car il permet, en principe, de dénombrer l'ensemble des structures possibles d'un langage.
Lorsque l'on a construit toutes les structures possibles d'un langage donné, on peut dire que l'on a en quelque sorte « épuisé » les possibilités de ce langage, atteint ses frontières internes, ses limites combinaitoires. Nous reviendrons sur ce point lorsque nous aborderons la notion de créativité.
Discussion Ce qui distingue la notion de langage d'un simple système de définitions intensives, c'est bien la présence d'une alternative entre différents symboles dans la construction des structures. Suivant les définitions précédemment posées, un langage comporte nécessairement une forme de classification, fût-elle artificielle. Si les structures engendrées sont des cas particuliers, le langage en est la généralisation, mettant en évidence leur pattern de construction.
Un langage sans possibilités reviendrait à une grammaire à production unique. En modifiant notre exemple précédent afin d'en faire une description structurelle fixe :
symbole : 1 structure : symbole*3
Nous nous retrouvons avec une seule structure autorisée, « 111 », qui d'un point de vue interne au langage ne se distingue d'aucune autre.
Un tel langage statique, ne comportant pas d'incertitude, rendrait toute communication inutile. En effet, si un langage n'autorise qu'une seule structure possible, ou si chaque signe n'a qu'une interprétation fixe et prévisible, alors la transmission n'apporte rien : le récepteur sait déjà ce que le message contient avant de le recevoir4c.
À l'instar des définitions dont il est l'extension, un langage peut lui aussi être envisagé à différents niveaux de relativité. À partir d'un langage donné, il est ainsi possible de définir des méta-langages ainsi que des proto-langages. Cette hiérarchie de niveaux découle des choix d'interprétation qui sont posés et peut être réalisée de multiples façons.
Exemple Dans l'exemple suivant, un mot est une combinaison de lettres. À partir de ce langage fondamental, nous pouvons construire un méta-langage dans lequel une phrase est un agencement de mots4d.
lettre : a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z mot : lettre* phrase : mot⊛
Cette latitude dans le niveau d'analyse se reflète d'ailleurs dans la manière dont l'alphabet du langage peut être défini : on peut distinguer plusieurs ensembles de départ, les regrouper, ou bien définir des niveaux intermédiaires.
Exemple Voici un autre langage permettant de générer des mots, mais où les voyelles et les consonnes sont maintenant distinguées et classifiées :
voyelle : a | e | i | o | u | y consonne : b | c | d | f | g | h | j | k | l | m | n | p | q | r | s | t | v | w | x | z mot : (voyelle | consonne)*
Dans cette notation, un mot est formé formé par une répétition de consonnes ou de voyelles (ou les deux). C'est-à-dire qu'à chaque étape de construction, on prend soit une voyelle, soit une consonne. Mais on pourrait tout aussi bien pu ajouter un niveau intermédiaire à ce langage :
voyelle : a | e | i | o | u | y consonne : b | c | d | f | g | h | j | k | l | m | n | p | q | r | s | t | v | w | x | z lettre : voyelle | consonne mot : lettre*
La manière de définir un langage conduisant à un espace de structures donné n'est donc pas unique.
Discussion Mais pourrait-on toujours réduire un langage générant un espace de structures donné à une forme unique ? En effet, dans les exemples précédents, en développant la définition de mot nous trouvons à chaque fois cette forme condensée :
mot : (a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z)*
*) par rapport à une combinaison de mots (⊛) pour bien mettre en évidence le fait que les deux règles de combinaison puissent être différentes. ↩
↑
Anecdote Un aspect qui m'avait fasciné en découvrant la grammaire BNF est qu'il soit possible de définir la grammaire BNF elle-même au moyen de la notation BNF. La description du langage est donc écrite avec le langage décrit.
Dans cette section, nous allons réaliser quelque chose de similaire avec le formalisme introduit jusqu'ici. Pour comprendre comment cela est possible, il suffit d'interpréter la définition d'un langage de manière littérale : non plus uniquement comme une série d'instructions, mais comme une chaîne textuelle composée de divers caractères4e.
Exemple L'extrait suivant peut être considéré comme une chaîne de caractères composée des symboles symbole, :, 0, |, 1, structure et + ainsi que d'espaces et de sauts de ligne.
symbole : 0 | 1 structure : symbole + symbole
Si le contenu de l'encadré est envisagé comme une structure composée de divers caractères, il est donc possible de définir un langage qui permette de générer cette chaîne de caractères.
Exemple Prenons un exemple encore plus simple pour en comprendre le mécanisme :
alcool : gin | tequila
Pour générer cette alternative nous pourrions imaginer le méta-langage suivant (où je numérote chaque définition pour m'y référer ultérieurement) :
(1) alternative : mot + " : " + mot + " | " + mot (2) mot = lettre* (3) lettre = a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z
La règle (1) indique qu'une alternative est constituée d'un premier mot, suivi d'un caractère double-point, puis de deux mots séparés par une barre verticale (1). La règle (2) définit quant à elle un mot comme une combinaison de lettres, les lettres minuscules de l'alphabet (3).
Une difficulté importante dans ce type de réflexion est la distinction entre les symboles du langage défini et les symboles du langage définisseur. Pour éviter une confusion entre les deux, un caractère entre guillemets indique ici un caractère à écrire littéralement. Par exemple « " | " » est une instruction d'écrire le symbole barre droite avec une espace de chaque côté (symbole du langage), tandis que « | » seul symbolise une alternative selon notre convention (symbole qui définit le langage). Cette complexité est inhérente à tout langage qui se référencie lui-même, et est difficile à appréhender pour le cerveau humain4f.
Pour reconstruire la définition « alcool : gin | tequila » à partir de ce méta-langage :
alcool, gin et tequila. alcool au premier « mot », gin au second, et tequila au troisième :alternative => alcool + " : " + gin + " | " + tequila
Cette combinaison produit la chaîne de caractères « alcool : gin | tequila », qui est bien la définition initiale. Notons que ce méta-langage ne permet pas uniquement de construire cet exemple, mais également toutes sortes d'alternatives entre deux éléments.
Rien n'empêche de continuer ce processus itératif : à partir de ce méta-langage, on peut en définir un autre, un méta-méta-langage, qui génère à son tour les règles (1), (2) et (3). Autrement dit : le processus peut être poursuivi indéfiniment par niveaux successifs.
Analogie En programmation, certains langages sont dits d'ordre supérieur. Ils permettent d'utiliser les noms de fonctions comme n'importe quelle autre variable, ce qui permet notamment de créer des fonctions récursives4g. Le formalisme présenté dans cet essai est aussi en quelque sorte d'ordre supérieur : un langage peut être traité comme n'importe quelle autre structure.
Le fait qu'un langage se décrive lui-même, parle de lui-même, entraîne une forme d'auto-référence. Dans cette boucle discrète mais vertigineuse, c'est comme s'il le langage se reconnaissait dans les structures qu'il engendrait, devenant ainsi l'objet de sa propre construction, et peut-être même capable de modifier les règles qui le définissent.
Intuition On pressent alors que la notion d'auto-référence entretient un lien profond avec le concept de conscience : un langage qui se décrit lui-même semble, d'une certaine manière, « prendre conscience » de son propre fonctionnement.
(Lx.x x)(Lx.x x). Le second (Lx.x x) est une expression littérale donnée comme entrée au premier (Lx.x x), qui lui est une fonction. ↩4g. Ce qui fait également penser aux quines, des programmes informatiques qui, une fois exécutés, impriment leur propre code source. ↩
↑
3.328 – Si un signe n'a pas d'usage, il n'a pas de signification. Tel est le sens de la devise d'Occam. (Si tout se passe comme si un signe avait une signification, c'est qu'alors il en a une.) L. Wittgenstein, Tractatus Logico-Philosophicus (1921)
Méta Le formalisme introduit dans cet essai est lui-même un langage. Comme tout langage, il permet la construction de certaines structures. Cet espace de structures détermine ce qu'il est possible de penser via ce langage.
Dans cette section, nous allons délibérément explorer les limites de cette notation et examiner comment la pensée peut parfois se perdre dans les méandres qui en résultent.
Discussion Jusqu'à présent, nous avons considéré chaque définition, par exemple screwdriver : jus d'orange + vodka, comme étant unidirectionnelle. Mais le langage autorise aussi l'écriture de la définition converse jus d'orange + vodka : screwdriver. Y a-t-il une différence entre ces deux formulations ?
D'un côté, notre expérience quotidienne tend à confirmer qu'une de ces définitions sous-entend implicitement l'autre. Si je goûte un cocktail et découvre qu'il s'agit d'un mélange de vodka et de jus d'orange, je vais instinctivement penser à l'appelation screwdriver.
Il semble donc que cognitivement, une définition n'agisse pas simplement dans un sens unidirectionnel mais invoque une relation bidirectionnelle. D'un autre côté, malgré cette réciprocité cognitive, il est parfois nécessaire de maintenire une distinction claire et unidirectionnelle entre les termes dans un système formel.
Symbolisme Remarquons à cet effet que le symbole « : » n'a pas de direction privilégiée. Il présente une symétrie verticale, suggérant que les termes de chaque côté de ce signe sont interchangeables. En revanche, un symbole asymétrique comme « ::= », utilisé dans la grammaire BNF d'origine, indique plus clairement une relation d'assignation unidirectionnelle4h. Afin de réduire les ambiguïtés, une bonne pratique consite à opter autant que possible pour un symbole qui est à l'image de ce que l'on souhaite signifier4i.
DiscussionUne autre façon de rendre explicite le renvoi bidirectionnel entre deux symboles consiste à recourir à un système de définitions circulaires. Dans l'exemple suivant, brasier renvoie à incendie, qui lui-même renvoie à brasier :
brasier : incendie incendie : brasier

Dans ce cas, chaque mot semble désigner l'autre de manière réciproque, sans que l'une des définitions fournisse un éclaircissement réel ou une explication supplémentaire4j. Nous revisiterons ce point plus en détail ultérieurement.

Discussion Les définitions circulaires peuvent également être interprétées de manière plus subtiles ou paradoxales. C'est le cas lorsque qu'un terme renvoie à lui-même, ou qu'une structure inclut, dans sa propre définition, une référence à elle-même comme partie du tout.
ensemble de tous les ensembles : tous les ensembles + ensemble de tous les ensembles
Un exemple classique est « l'ensemble de tous les ensembles », de Bertrand Russell, dont la définition nous conduit directement à un paradoxe. L'ensemble des ensembles devrait par définition, inclure tous les ensembles possibles, y compris lui-même, parce que c'est un ensemble. Mais si l'ensemble des ensembles se contient lui-même, il devient à la fois partie de lui-même, et le tout.
Un autre cas exotique de définition circulaire auto-réferentielle, est celui où le terme défini ne renvoie à aucun concept externe, mais s'auto-définit totalement :
fractale : fractale
Dans cette définition, la fractale peut être conçue comme une structure fermée sur elle-même. L'ensemble et ses parties sont identiques, et il n'y a pas de distinction possible entre ce qu'est une fractale et ce que l'on entend par le terme « fractale ». Ce type de définition nous amène à une clôture cognitive, où le système de signification s'auto-inclut de manière infinie et sans fin. On peut également voir cette définition comme symbolisant une boucle infinie où il n'y a ni point d'entrée ni de point de sortie pour la définition : la fractale est la fractale.
Enfin, nous pourrions encore discuter d'autres cas extrêmes comme celles de définitions « incomplètes », où un symbole ne renvoie à rien « brasier : », voire même une définition vide « : ». ❖
Dans toutes de ces discussions, le fait que notre notation graphique permette de produire des structures distinctes, nous pousse à nous interroger sur le sens de ces distinctions. Outre la satisfaction intellectuelle procurée par l'exploration des potentialités d'un langage, repousser les limites d'un système est un exercice qui oblige à examiner la robustesse de nos concepts et à enrichir notre compréhension.
Toutefois, une telle minutie peut rapidement se transformer en piège intellectuel. Le danger dans ce cas, est de s'enliser dans une spirale de questionnements stériles, prisonnier d'un formalisme vide de sens, qui bien que fascinant, n'aboutit à rien de productif 4k. Pour éviter cet écueil, il est crucial de rester ancré dans la réalité et de ne pas s'attarder indéfiniment sur des cas aussi extrêmes, sauf si l'on cherche à démontrer un point précis dans un cadre spécifique.
Pour éviter de créer des structures insensées dans un langage, on peut dès lors renforcer les contraintes formelles de ce langage en excluant certaines structures.
Exemple Je peux décider de rendre ma notation formelle stricte en interdisant les définitions circulaires ou vides.
Autrement dit, une structure d'un langage n'aura de sens que si nous décidons de lui en attribuer un.
= », est utilisé pour les deux. Comparons par exemple la différence de signification entre l'expression « f(x) = x2 », et l'expression « f(x) = g(x) ». À cet égard, je préfère nettement l'approche de la programmation où le symbole d'égalité représente toujours une affectation. ↩4i. Bien sûr, rien ne nous empêche de convenir qu'un symbole non symétrique comme « ::= » représente une relation symétrique entre deux symboles. Ce ne serait certes pas judicieux, mais possible. ↩4j. Lorsque deux mots, ou symboles, ont vocation à se substituer l'un à l'autre, on peut les qualifier de synonymes. Toutefois, il est crucial de se rappeler que cette synonymie est toujours relative à l'usage que l'on en fait et au niveau de détail que l'on considère. Par exemple, dans certains contextes, « brasier » et « incendie » peuvent être utilisés de manière interchangeable, mais dans d'autres, ces termes peuvent impliquer des nuances spécifiques. Un « brasier » par exemple peut être perçu comme un incendie de grande ampleur. ↩4k. Anecdote En philosophie, l'exemple classique est pour moi l'ergotage entre le sens du mot « être » et le sens du mot « avoir ». Cela me rappelle une professeure de français qui nous avait enseigné la différence entre « convaincre » et « persuader » : l'un amènerait quelqu'un à changer d'opinion via des arguments rationnels, l'autre via les émotions. Un usage qu'en pratique personne ne fait de ces deux mots et donc une distinction artificielle et inutile. ↩
↑
Physicists observe the phenomena of nature and try to find patterns that relate these phenomena. These patterns are called physical theories or, when they are very well established and widely used, physical laws or principles. H. D. Young & R. A. Freedman, Sears and Zemansky's University physics with modern physics (2012)
Nous avons pour habitude de dire qu'il y a différentes sortes d'intelligences. Dans cet essai cependant, j'essaye de ramener toutes les intelligences à un dénominateur commun. En ce sens, je dirais plutôt qu'il y a différents langages, qui partagent des mécanismes communs, et que plus on maîtrise un langage en particulier et plus on fait preuve d'intelligence par rapport à ce langage.
Idée S'il y a effectivement une unité dans l'intelligence, la maîtrise d'un langage devrait renforcer la maîtrise des autres.
Parmi les compétences qui me semblent constitutives de l'intelligence, la première est la reconnaissance des structures d'un langage.
Anecdote On m'a un jour présenté une photographie d'un acarien à l'échelle microscopique. Au premier regard, mon cerveau ne parvenait pas à donner sens à cette image. Ce n'est qu'après quelques secondes que je suis parvenu à distinguer les différentes parties de l'arachnide. Cet exemple illustre la différence entre le simple fait d'observer un ensemble de symboles, et celui d'y percevoir une structure.
Cette capacité à reconnaître des structures suppose souvent un apprentissage préalable.
Exemple Lorsqu'on ne connaît pas les sons produits par une basse, on ne prête pas forcément attention à la ligne de basse dans une chanson. De même, lorsqu'on pratique la peinture, on développe un vocabulaire associé aux couleurs (nom des pigments, code, nuances, etc.) qui permet de les distinguer plus finement.
Discussion S'il est nécessaire d'avoir été initié à la reconnaissance d'une structure pour pouvoir le repérer au sein d'un ensemble de symboles, comment a pu émerger la « première » forme d'intelligence ?
Outre la faculté de reconnaître des structures, une autre composante essentielle de l'intelligence serait la détection de patterns récurrents entre différentes structures. C'est-à-dire la capacité à généraliser en établissant des classifications, des abstractions.
Exemple Lorsqu'on apprend à reconnaître différentes espèces d'arbres, on commence par identifier les feuilles, les fruits, les fleurs, les troncs ou les silhouettes propres à chacune. Mais avec l'expérience, on remarque des ressemblances structurelles entre certaines familles d'arbres et l'on finit par regrouper ces observations en classifications plus générales : feuillus, conifères, etc.
Définition J'appelle intelligence la capacité à repérer des structures et des patterns4l.
Discussion Je réduis ici volontairement l'intelligence à une faculté fondée uniquement sur l'observation, et non sur la manipulation de symboles ou la transformation de structures. En effet, la reconnaissance de structures et de patterns par un agent4m ne suppose a priori aucune interaction avec l'environnement, si ce n'est celle strictement nécessaire à l'acte d'observation.
Discussion La capacité à reconnaître des structures et des patterns, soulève une question intéressante : quelles seraient les conditions pour qu'un agent puisse reconstruire un langage, c'est-à-dire déduire ses symboles et ses règles de combinaison, à partir de l'observation de certaines structures générées via ce langage ?
Suivant ce prisme d'analyse de l'intelligence, j'aimerais proposer une définition partielle de la science : il s'agirait de toute discipline dont l'objectif est de décrire des structures et repérer des patterns au sein d'un langage. Le point intéressant est que cette définition ne dépend plus du domaine considéré : il est ainsi possible d'adopter une démarche scientifique par rapport à n'importe quel sujet.
Discussion Cette approche purement structurale laisse cependant de côté un attribut essentiel que l'on associe à la science : l'adéquation avec la réalité. En effet, la faculté de décrire des structures et détecter des patterns ne dit encore rien sur la validité des symboles, leur correspondance avec le réel. Pour différencier une science au sens usuel d'une pseudo-science, il manque donc des dimensions supplémentaires de confrontation empirique, de contrôle expérimental, et d'esprit critique. Mais ça c'est le sujet d'un autre livre.
Exemple Je peux imaginer un modèle physique dans lequel la force ne serait pas proportionnelle à l'accélération mais proportionnelle à la vitesse, c'est-à-dire F = mv à la place de F = ma. Je peux m'amuser à développer ce modèle et imaginer comment serait l'univers si une telle loi existait. Peut-on appeler un modèle qui part de prémisses fausses pour aboutir logiquement à des conclusions vraies une science ?
Séparer la dimension structurante de la science de son rapport à la vérité permet de comprendre comment des disciplines comme l'alchimie ont pu être considérées comme scientifiques dans le passé mais ont perdu ce statut aujourd'hui : elles mettaient effectivement en œuvre une recherche de structures, mais à partir de prémisses fausses4n. Plus généralement, cela rappelle que l'on peut consacrer une vie entière à explorer de façon rigoureuse un système erroné, exercer son intelligence à chercher des explications et des connexions au sein d'un matériel de base fallacieux4o.
Pourtant, la frontière entre science et non-science n'est pas toujours aussi simple à délimiter sur base du seul critère d'adéquation au réel : le degré de rigueur interne, de cohérence logique et de puissance générative du langage employé jouent également un rôle dans cette classification.
Exemple Il existe des disciplines rigoureusement structurées qui ne visent pas directement la description du monde mais dont la valeur scientifique me semble difficilement contestable. La géométrie hyperbolique, par exemple, n'avait pas pour vocation de décrire directement le réel car elle était issue d'une variation des postulats euclidiens. Longtemps considérée comme une curiosité formelle, elle s'est révélée ultérieurement pertinente pour la description de l'espace physique relativiste. De même, la théorie des nombres explore des régularités abstraites au sein du langage mathématique, sans rapport immédiat avec la réalité empirique. Mais ses résultats trouvent parfois, des décennies plus tard, des applications inattendues.
6.211 – Dans la vie, ce n'est pas de propositions mathématiques dont nous avons besoin, mais nous usons de la proposition mathématique, pour déduire, de propositions qui n'appartiennent pas à la mathématique, d'autres propositions qui ne lui appartiennent pas non plus. L. Wittgenstein, Tractatus Logico-Philosophicus (1921)
Quel est l'intérêt pratique à utiliser un formalisme, tel que celui décrit dans ce texte ? Et de manière plus générale, quel est l'intérêt d'utiliser des systèmes « abstraits » de signes graphiques ?
L'intérêt c'est que s'il est possible d'établir une correspondance (ou isomorphisme4p) entre un système symbolique et des entités physiques, il est généralement plus facile, efficace, de manipuler le système symbolique plutôt que les entités physiques qu'elles représentent.
Exemple Il est beaucoup plus facile pour un être humain d'additionner le nombre 1415 au nombre 9265 à travers une manipulation de symboles, mentale ou écrite, plutôt que de réunir physiquement 1415 vaches et 9265 moutons dans un champ et de compter le nombre total qui en résulte.
Plus généralement, en établissant une correspondance entre les symboles, règles de combinaison, ou structures d'un langage, avec les symboles, règles de combinaison ou structures d'un autre langage, il est possible de manipuler les symboles de l'un afin de réaliser des déductions dans l'autre, et vice-et-versa.

ExempleDans la vie quotidienne, il nous arrive souvent de devoir trouver notre chemin, une adresse, dans une grande ville. Nous utilisons pour cela des cartes, qui sont une représentation symbolique de la ville : une rue peut être représentée par deux lignes droites, des immeubles par des quadrilatères. Bien que la carte ne représente pas physiquement la ville, le fait qu'il existe une correspondance entre le système graphique (la carte) et le monde réel (la ville) nous permet de nous repérer dans l'espace urbain de manière beaucoup plus simple que si nous devions comprendre la ville dans sa totalité à chaque fois.
Exemple En physique, une telle correspondance est une pratique courante dans l'analyse des signaux. Plutôt que de travailler sur un signal dans le domaine temporel, on le convertit dans le domaine des fréquences grâce à une transformée de Fourier ou de Laplace. Dans cette nouvelle représentation, certaines opérations deviennent beaucoup plus simples à effectuer : des convolutions deviennent des multiplications, des dépendances temporelles deviennent des rapports de fréquence. Une fois les calculs effectués, on « revient » dans le langage initial, celui du temps, en appliquant la transformée inverse. Ainsi, on tire parti d'un isomorphisme entre deux systèmes symboliques pour résoudre plus aisément un problème qui, dans son domaine d'origine, serait beaucoup plus difficile à traiter.
Pattern Naviguer entre des langages, ou entre des niveaux hiérarchiques différents, est un pattern récurrent dans nos vies. Voici quelques exemples de ces va-et-vients, dont certains que nous avons déjà rencontrés dans cet essai :
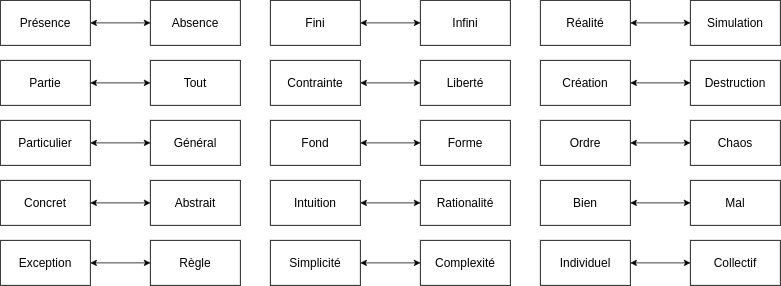
Ce qui est particulièrement profond dans ces aller-retours entre deux langages, c'est qu'ils nous permettent de rapporter quelque chose de nouveau dans le langage initial.