Les Empreintes – Essai de théorie musicale


L'idée d’écrire un essai de théorie musicale s'insinua en moi pour la première fois à un moment de ma vie où j'avais décidé de m’intéresser à des aspects de la musique qui m’avaient toujours paru hermétiques : le jazz et la composition. Il s'ensuivit une période d'effervescence où je dévorais les classiques du jazz les uns après les autres, constamment penché sur ma guitare.

Ressentant le besoin de synthétiser et d'explorer ces nouvelles directions musicales, je m'attelai à la rédaction d'un premier projet : réaliser une sorte de catalogue des positions des gammes et des accords à la guitare. Par exemple, j'étais intrigué par la possibilité d'établir un inventaire exhaustif des modes, ou encore des gammes construites à partir d'une répétition d'intervalles.
Vue cette ampleur ambitieuse grandement influencée par les mathématiques1, et absorbé par la vie étudiante, je laissai bien vite cette entreprise chronophage en suspend. Mais au fil des mois et des années, j'allais revenir régulièrement à ce projet obsédant qui me conduisit à penser les gammes de manière abstraite. En effet, sur une guitare, une fois la position d'une gamme particulière connue pour une certaine note de départ, il suffit de décaler celle-ci sur le manche pour la transposer automatiquement à d'autres tonalités. Je n'étais donc pas tant intéressé par la position d'une gamme pour une tonalité en particulier, mais plutôt par le « schéma » de cette gamme.
C'est alors qu'au beau milieu d'une nuit d'insomnie, je réalisai qu'il était très simple de dénombrer l'ensemble des gammes : entre une note et son octave, il y a 11 notes chromatiques. Par conséquent, pour former une gamme à partir d'une note donnée, je peux choisir d'inclure ou non chacune de ces 11 notes, ce qui me donne 11 choix binaires à effectuer. Autrement dit, à partir d'une note déterminée, il existe $2^{11} = 2048$ gammes différentes.
C'est ainsi que nacquit le concept d'empreinte d'une gamme : un nombre binaire symbolisant de manière unique la suite d'intervalles d'une gamme. Ainsi deux gammes ayant la même suite d'intervalles, comme par exemple Do majeur et Ré majeur, se traduisent par la même empreinte, c'est-à-dire le même pattern ou « patron de gamme ». L'idée de marier musique et informatique ayant également fait son chemin, et abandonnant l'approche guitaristique je me mis alors à écrire un programme afin de répertorier les empreintes et pouvoir les analyser.
Dans cet essai, je vous présente donc le résultat de ces pérégrinations musicales. J'attire l'attention sur le fait que le résultat final est un traité de théorie musicale abstraite, à la frontière entre mathématiques et musique : j'explore les propriétés qui découlent d'un modèle simple, sans but immédiat de proposer des applications pratiques. Comme prérequis, une connaissance de base en théorie musicale est nécessaire, ainsi qu'une curiosité sur le sujet du recensement des gammes.
Dans ce chapitre, je vais définir le concept d'empreinte. Pour cela, je vais commencer par simplifier grandement la complexité musicale en posant comme hypothèse de base qu'il n'y a que 12 notes distinctes.
Hypothèse 1 Je considère qu'il n'existe que 12 notes distinctes formant une liste circulaire ordonnée avec un sens de parcours privilégié :
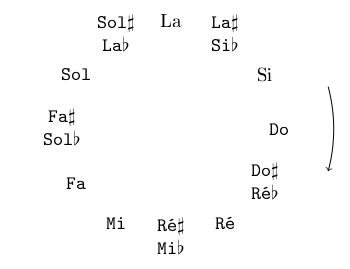
Je réalise donc un important réductionnisme méthodologique en ne distinguant pas les notes enharmoniques, ce qui simplifie la tâche, mais occulte en contrepartie tout un pan de la richesse musicale. Cette simplification relève d'une réalité pratique de certains instruments qui n'ont pas la possibilité de faire entendre facilement la différence entre deux notes enharmoniques, comme par exemple la guitare et le piano. Faute d'une meilleure terminologie2, je conserve cependant la possibilité d'utiliser les deux dénominations enharmoniques : on pourra donc utiliser indifféremment la notation avec bémol (♭) ou celle avec dièse (♯).
Je vais par ailleurs ignorer la réalité physique des notes, et considérer qu'a priori, ces 12 notes sont simplement une collection d'objets abstraits ayant certaines propriétés. En pratique cela signifie que je ne rentrerai pas dans des considérations évoquant par exemple la fréquence des notes, leur timbre, le tempérament des instruments ou encore la perception psychoacoustique des sons.
Notons que le fait de définir un sens de parcours privilégié des notes est simplement une commodité qui permet d'éviter d'alourdir inutilement les définitions en considérant à chaque fois les deux sens de parcours possibles.
Maintenant que nos 12 symboles de base ont été déterminés, je vais maintenant spécifier la manière dont il est possible de créer des gammes à partir d'eux.
Hypothèse 2 À partir d'une note de départ quelconque, il est possible d'y juxtaposer les autres notes dans l'ordre de parcours privilégié jusqu'à revenir à la note de départ, ce qui engendre une suite linéaire de 13 notes consécutives.
Exemple Voici la suite linéaire de 13 notes consécutives démarrant et se terminant par la note Ré :
| Ré | Ré♯ | Mi | Fa | Fa♯ | Sol | Sol♯ | La | La♯ | Si | Do | Do♯ | Ré |
Définition J'appelle gamme chromatique une telle suite linéaire de 13 notes consécutives. La première note d'une gamme chromatique est appelée tonique et la dernière octave.
Puisque nous pouvons écrire une gamme chromatique à partir de n'importe laquelle de nos 12 notes, nous distinguons donc 12 notes chromatiques différentes. Rien de suprenant jusqu'ici.
La gamme chromatique ayant été définie, je voudrais maintenant donner une définition pratique d'une gamme en général pour le cadre de cette étude.
Définition Une gamme est tout sous-ensemble de notes issue d'une gamme chromatique, comprenant sa tonique et son octave.
Exemple La gamme de Do majeur peut être vue comme un sous-ensemble de la gamme chromatique de Do.
| Do | Do♯ | Ré | Ré♯ | Mi | Fa | Fa♯ | Sol | Sol♯ | La | La♯ | Si | Do |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | |||||
| Do | Ré | Mi | Fa | Sol | La | Si | Do |
À partir de symboles de base, les notes, nous avons défini des structures, les gammes. La prochaine étape consiste à spécifier les relations existant entre les notes au sein des gammes.
Hypothèse 3 Je définis l'existence entre les notes d'une propriété appelée distance musicale ou intervalle dont l'unité de mesure est appelée demi-ton.
Dans une gamme chromatique :
Dans une gamme quelconque, l'intervalle entre 2 notes est égal à l'intervalle entre les 2 notes dans une gamme chromatique. ❖
Exemple Dans une gamme chromatique les intervalles entre notes consécutives valent toujours 1 demi-ton : $$Do \overset{1}{\longleftrightarrow} Do\sharp{} \overset{1}{\longleftrightarrow} Ré \overset{1}{\longleftrightarrow} Ré\sharp{} \overset{1}{\longleftrightarrow} Mi \overset{1}{\longleftrightarrow} Fa \overset{1}{\longleftrightarrow} Fa♯ \overset{1}{\longleftrightarrow} \dots{} $$
Entre $Do$ et $Mi$, il y a donc 4 demi-tons : $$Do \overset{4}{\longleftrightarrow} Mi $$
ExempleVoici les intervalles de la gamme pentatonique mineure de $La$ : $$La \overset{3}{\longleftrightarrow} Do \overset{2}{\longleftrightarrow} Ré \overset{2}{\longleftrightarrow} Mi \overset{3}{\longleftrightarrow} Sol \overset{2}{\longleftrightarrow} La$$
En effet, ceux-ci correspondent à la somme des intervalles entre les notes dans une gamme chromatique : $$La \overset{1}{\longleftrightarrow} La♯ \overset{1}{\longleftrightarrow} Si \overset{1}{\longleftrightarrow} Do$$ $$Do \overset{1}{\longleftrightarrow} Do♯ \overset{1}{\longleftrightarrow} Ré$$ $$Ré \overset{1}{\longleftrightarrow} Ré♯ \overset{1}{\longleftrightarrow} Mi$$ $$etc.$$
❖
Au sein d'une gamme, l'intervalle maximum possible est de 12 demi-ton : c'est l'intervalle entre la tonique et l'octave. L'intervalle minimum est un intervalle conceptuel nul de 0 demi-ton, c'est-à-dire l'intervalle fictif entre une note et elle-même. Je vais maintenant une introduire une notation pour les intervalles en fonction de leur longueur.
Notation Voici un tableau donnant la dénomination et l'abréviation des intervalles en fonction de leur longueur :
| Demi-ton | Dénomination | Abréviation |
|---|---|---|
| 0 | Unisson | U |
| 1 | Seconde mineure (demi-ton) | s |
| 2 | Seconde majeure (ton) | S |
| 3 | Tierce mineure | t |
| 4 | Tierce majeure | T |
| 5 | Quarte juste | q |
| 6 | Quarte augmentée (triton) Quinte diminuée | Q |
| 7 | Quinte juste | $\bar{q}$ |
| 8 | Sixte mineure | $\bar{T}$ |
| 9 | Sixte majeure | $\bar{t}$ |
| 10 | Septième mineure | $\bar{S}$ |
| 11 | Septième majeure | $\bar{s}$ |
| 12 | Octave | $\bar{U}$ |
Exemple Voici les intervalles de la gamme pentatonique mineure de $La$ écrits avec cette notation : $$La \overset{t}{\longleftrightarrow} Do \overset{S}{\longleftrightarrow} Ré \overset{S}{\longleftrightarrow} Mi \overset{t}{\longleftrightarrow} Sol \overset{S}{\longleftrightarrow} La$$
Contexte Cette notation est empruntée à la théorie des groupes en mathématiques3 afin de dénoter les éléments symétriques. On a en effet: $$s + \bar{s} = t + \bar{t} = T + \bar{T} = q + \bar{q} = Q + Q = U$$
Nous allons maintenant pouvoir définir aisément la notion d'empreinte.
Définition J'appelle empreinte la suite d'intervalles caractéristiques d'une gamme.
Exemple L'empreinte de la gamme de Do majeur est $\langle SSsSSSs \rangle$, qui se lit « ton, ton, demi-ton, ton, ton, ton, demi-ton ». En effet, il s'agit des intervalles constituant la gamme : $$Do \overset{S}{\longleftrightarrow} Ré \overset{S}{\longleftrightarrow} Mi \overset{s}{\longleftrightarrow} Fa \overset{S}{\longleftrightarrow} Sol \overset{S}{\longleftrightarrow} La \overset{S}{\longleftrightarrow} Si \overset{s}{\longleftrightarrow} Do$$
Notation J'indique les empreintes entre crochets $\langle \rangle$ et lorsque cela s'avère opportun, j'abrège les intervalles identiques consécutifs par une notation à exposant.
ExempleJ'écris l'empreinte d'une gamme chromatique $\langle s^{12} \rangle$ à la place de $\langle ssssssssssss \rangle$.
Le concept d'empreinte est une abstraction qui généralise le concept de gamme. En effet, il existe 12 versions de chaque gamme, une distincte par note de départ. Si nous nous intéressons uniquement aux intervalles que contient une gamme, il nous importe peu de savoir laquelle de ces 12 gammes nous considérons en particulier. Ce qui nous intéresse ce sont ce que ces gammes ont en commun, c'est-à-dire la structure de leurs intervalles, leur empreinte.
À partir d'une empreinte donnée, il est possible d'instancier n'importe laquelle des 12 gammes correspondantes. Voici un schéma dépeignant le processus :
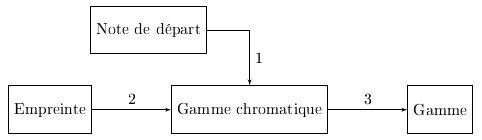
ExempleEn choisissant $La$ comme note de départ, et l'empreinte de la gamme mineure harmonique $\langle SsSSsts \rangle$ nous construisons la gamme mineure harmonique de $La$ à l'aide du tableau suivant :
| 1. | La | La♯ | Si | Do | Do♯ | Ré | Ré♯ | Mi | Fa | Fa♯ | Sol | Sol♯ | La |
| 2. | ↓ | S | s | S | S | s | t | s | |||||
| 3. | La | Si | Do | Ré | Mi | Fa | Sol♯ | La |
La gamme de $La$ mineure harmonique est donc : La Si Do Ré Mi Fa Sol♯ La. ❖
Dans cette optique, il me paraît plus approprié de parler de « gamme mineure harmonique de $La$ » plutôt que de « gamme de $La$ mineure harmonique ». Je suivrai donc cette convention dans le reste de ce texte.
↑Nous sommes maintenant familiarisés avec la représentation des empreintes comme une suite d'intervalles. Mais il est également possible de représenter une empreinte par une suite de notes abstraites.
Notation Voici une représentation abstraite, ou fonctionnelle, des 13 notes d'une gamme chromatique :
| 1v | 2m | 2M | 3m | 3M | 4j | 4q | 5j | 6m | 6M | 7m | 7M | 8v |
L'intêrét de cette notation, c'est qu'elle ne dépend plus d'une note de départ. Deux gammes ayant la même empreinte auront aussi la même notation fonctionnelle.
ExempleReprenons l'exemple précédent où nous avions dérivé la gamme mineure harmonique de $La$ à partir de son empreinte $\langle SsSSsts \rangle$. Cette fois, nous substituons la gamme chromatique de $La$ par sa notation fonctionnelle (ligne 1') e qui nous donne la notation fonctionnelle d'une gamme mineure harmonique (ligne 3') :
| 1. | La | La♯ | Si | Do | Do♯ | Ré | Ré♯ | Mi | Fa | Fa♯ | Sol | Sol♯ | La |
| 1'. | 1v | 2m | 2M | 3m | 3M | 4j | 4q | 5j | 6m | 6M | 7m | 7M | 8v |
| 2. | ↓ | S | s | S | S | s | t | s | |||||
| 3'. | 1v | 2M | 3m | 4j | 5j | 6m | 7M | 8v | |||||
| 3. | La | Si | Do | Ré | Mi | Fa | Sol♯ | La |
D'où la notation fonctionnelle d'une gamme mineure harmonique : 1v 2M 3m 4j 5j 6m 7M 8v. ❖
Dans cette notation abstraite, le symbole 1v représente la note de départ tandis que les autres symboles représentent les sommes cumulées des intervalles de la gamme. Il existe en effet une correspondance entre la notation des intervalles et celles des notes fonctionnelles :
| U | s | S | t | T | q | Q | $\bar{q}$ | $\bar{T}$ | $\bar{t}$ | $\bar{S}$ | $\bar{s}$ | $\bar{U}$ |
| 1v | 2m | 2M | 3m | 3M | 4j | 4q | 5j | 6m | 6M | 7m | 7M | 8v |
Cette différence de notation est là pour distinguer clairement le point de vue des intervalles du point de vue des notes fonctionnelles.
Il nous est donc maintenant possible de représenter des empreintes, non seulement par une suite d'intervalles mais également par une suite de notes abstraites. Il existe donc deux manières complémentaires d'aborder une empreinte : soit via ses notes, soit via ses intervalles. En effet, bien que le point des vues des intervalles permettent une pensée plus abstraite, notre système musical fait que nous avons plutôt tendance à penser en termes de notes d'où l'intérêt d'une telle notation.
Notons enfin que puisque l'octave représente symboliquement la même note que la tonique, on peut en omettre le symbole (8v), et considérée qu'elle est implicitée.
Exemple L'empreinte majeure peut se noter soit par ses intervalles $\langle SSsSSSs \rangle$, soit par ses notes fonctionnelles : 1v 2M 3M 4j 5j 6M 7M.
↑Now I realize that many people, when they see a generating function coming in their direction, will cross to the other side of the street to avoid it. Herbert S. Wilf, Lectures on integer partition (2000)
Dans ce chapitre, je vais montrer comment il est possible de dénombrer l'ensemble des empreintes et proposer ensuite un système de classement de celles-ci, basée sur la notion de mode, puis sur le concept de partition.
Pour dénombrer le nombre d'empreintes différentes existantes, il faut penser à la manière dont nous pouvons créer une empreinte quelconque à partir des notes fonctionnelles de l'empreinte chromatique : 1v 2m 2M 3m 3M 4j 4q 5j 6m 6M 7m 7M. Puisque toute empreinte contient au moins une note, la tonique, chaque empreinte contient d'office 1v. Pour créer une empreinte en particulier, il nous reste donc à décider quelles notes parmi les 11 restantes nous allons inclure dans l'empreinte :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2m | 2M | 3m | 3M | 4j | 4q | 5j | 6m | 6M | 7m | 7M |
Pour chacune de ces notes fonctionnelles, nous pouvons choisir soit de l'inclure dans l'empreinte, soit de ne pas l'inclure, ce qui revient à effectuer 11 choix binaires.
Résultat Le nombre d'empreintes distinctes est donné par le nombre de 11-tuples binaires, soit : $$2^{11} = 2048$$
Le corollaire de ce résultat, c'est qu'il est possible d'écrire chaque empreinte sous la forme d'un nombre binaire à 11 chiffres. Voici comment faire :
Exemple Voici comment construire la représentation binaire de l'empreinte majeure (1v 2M 3M 4j 5j 6M 7M) :
| 1. | 1v | 2m | 2M | 3m | 3M | 4j | 4q | 5j | 6m | 6M | 7m | 7M |
| 1v | 2M | 3M | 4j | 5j | 6M | 7M | ||||||
| 2. | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
L'empreinte majeure est donc représentée par le nombre binaire $\langle 01011010101 \rangle$. ❖
L'intérêt de cette notation binaire est double. Premièrement, cela permet d'utiliser la programmation afin de répertorier l'ensemble des 2048 empreintes et de les manipuler. Deuxièmement celle-ci permet de numéroter de manière unique chaque empreinte par un nombre allant de 0 à 2047, et ce en convertissant la représentation binaire d'une empreinte vers une base décimale.
Exemple L'empreinte majeure est la numéro 725 car $01011010101_2 = 725_{10}$.
La prochaine question qui me taraudait était de savoir comment se répartissaient ces 2048 empreintes en fonction de leur nombre de notes.
Résultat Le nombre d'empreintes distinctes à $n$ notes est donnée par le nombre de combinaisons possibles de $n - 1$ notes parmi 11, soit : $$C_{11}^{n-1} = \frac{11!}{(12 - n)! \cdot (n - 1)!}$$
À l'aide de cette formule, il est possible de former le tableau suivant qui donne la répartition des empreintes en fonction du nombre de notes :
| Notes $n$ | Empreintes $C_{11}^{n-1}$ |
|---|---|
| 1 | 1 |
| 2 | 11 |
| 3 | 55 |
| 4 | 165 |
| 5 | 330 |
| 6 | 462 |
| 7 | 462 |
| 8 | 330 |
| 9 | 165 |
| 10 | 55 |
| 11 | 11 |
| 12 | 1 |
Nous constatons que la répartition des empreintes est symétrique4 et que les empreintes les plus nombreuses sont celles à 6 et 7 notes. Dans les chapitres ultérieurs de cet essai, je m'attache à explorer ces répartitions afin de dégager les empreintes intéressantes d'un point de vue musical. Mais avant cela, j'aimerais organiser ces différentes empreintes.
La première idée qui m'est venue à l'esprit concernant un critère de classification des empreintes a été d'utiliser la notion de mode.
Définition Deux empreintes sont dites modes l'une de l'autre s'il est possible de générer l'une d'elle à partir de permutations cycliques des intervalles de l'autre. J'appelle famille l'ensemble des empreintes qui sont des modes l'une de l'autre.
Exemple Voici l'ensemble des permutations cycliques de l'empreinte majeure $\langle SSsSSSs \rangle$ :
| I | S S s S S S s |
| II | S s S S S s S |
| III | s S S S s S S |
| IV | S S S s S S s |
| V | S S s S S s S |
| VI | S s S S s S S |
| VII | s S S s S S S |
Il s'agit bien entendu des 7 empreintes des modes de la gamme majeure : ionien, dorien, phrygien, lydien, myxolydien, æolien et locrien. Ces 7 empreintes forment une famille, qu'on pourrait appeler « famille majeure ». ❖
Une fois le concept de famille défini, nous aimerions maintenant savoir combien de familles différentes il existe parmi toutes les empreintes. Comme je ne trouvais pas de formule évidente permettant de les dénombrer, j'ai donc décider de les recenser empiriquement via un script informatique.
Résultat Je trouve empiriquement qu'il existe 351 familles différentes.
Il suffit donc d'un noyau de 351 empreintes judicieusement choisies afin de générer l'ensemble des 2048 empreintes. Pour savoir comment se répartissaient ces familles en fonction du nombre de notes de l'empreinte, j'ai opté une fois de plus pour une approche pragmatique et ai eu recours à la programmation. Voici le tableau précédent mis à jour avec la répartition des familles en fonction du nombre de notes :
| Notes $n$ | Empreintes $C_{11}^{n-1}$ | Familles |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 11 | 6 |
| 3 | 55 | 19 |
| 4 | 165 | 43 |
| 5 | 330 | 66 |
| 6 | 462 | 80 |
| 7 | 462 | 66 |
| 8 | 330 | 43 |
| 9 | 165 | 19 |
| 10 | 55 | 6 |
| 11 | 11 | 1 |
| 12 | 1 | 1 |
Ici aussi apparaît une distribution symétrique (en omettant l'empreinte chromatique à 12 notes), centrée autour des empreintes à 6 notes qui contiennent le plus grand nombre de familles.
Discussion Afin d'approximer ces résultats, il est possible de généraliser abusivement le cas de l'empreinte majeure qui a 7 notes et engendre 7 modes. En effet, en général, une empreinte à $n$ modes est génératrice de $n$ modes. Je dis bien en général car comme nous le verrons par la suite, certaines empreintes dérogent à cette règle. Nous pouvons ainsi estimer le nombre de familles par nombre de notes en divisant le nombre d'empreintes par le nombre de notes, c'est-à-dire $C_{11}^{n-1} / n $ :
| Notes $n$ | Empreintes $C_{11}^{n-1}$ | Familles | $C_{11}^{n-1} / n $ |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 11 | 6 | 5,5 |
| 3 | 55 | 19 | 18,333.. |
| 4 | 165 | 43 | 41,25 |
| 5 | 330 | 66 | 66 |
| 6 | 462 | 80 | 77 |
| 7 | 462 | 66 | 66 |
| 8 | 330 | 43 | 41,25 |
| 9 | 165 | 19 | 18,333.. |
| 10 | 55 | 6 | 5,5 |
| 11 | 11 | 1 | 1 |
| 12 | 1 | 1 | 0,0833.. |
Cette formule fonctionne pour les empreintes à 1, 5, 7 et 11 notes. Pour les autres en revanche (empreinte chromatique mise à part), nous voyons que les prédictions ne collent pas aux résultats mais constituent néanmoins une bonne approximation. Ce constat nous amène à la conclusion suivante : il existe des empreintes dont le nombre de modes est inférieur au nombre de notes. J'explorerai plus en profondeur ces empreintes dans un chapitre ultérieur. ❖
↑Pour aller encore plus loin dans la classification des empreintes, je vais introduire la notion de partition d'un entier.
Définition En mathématiques, une partition d'un entier est une décomposition de cet entier en une somme d'entiers strictement positifs.
Exemple Il existe 7 partitions de l'entier 5. Les voici : $$\begin{eqnarray} 5 &=& 5 \\ &=& 4 + 1 \\ &=& 3 + 2 \\ &=& 3 + 1 + 1 \\ &=& 2 + 2 + 1 \\ &=& 2 + 1 + 1 + 1 \\ &=& 1 + 1 + 1 + 1 + 1 \end{eqnarray}$$
Notons que dans une partition, l'ordre des termes de la somme ne compte pas. Par exemple, $4 + 1$ et $1 + 4$ représentent la même partition. ❖
Maintenant que nous savons ce qu'est une partition d'un entier, nous allons pouvoir appliquer cette notion aux empreintes. De la tonique à l'octave, la somme des intervalles d'une empreinte vaut toujours 12 demi-tons car l'intervalle d'octave est composé de 12 demi-tons. Par conséquent, chaque empreinte correspond à une partition du nombre 12 et nous pouvons donc classer les empreintes en fonction de la partition à laquelle elles appartiennent.
Exemple L'empreinte pentatonique mineure est $\langle tSStS \rangle$. Convertissons ces intervalles en nombre de demi-ton :
| t | S | S | t | S |
| 3 | 2 | 2 | 3 | 2 |
Ce qui nous donne bien la partition $3 + 2 + 2 + 3 + 2 = 12$. ❖
On notera que tous les modes d'une empreinte appartiennent forcément à la même partition, puisque changer l'ordre des intervalles n'a pas d'influence sur la partition. Par contre, là où le concept de partition réduit la complexité du concept de famille, c'est que plusieurs familles peuvent appartenir à la même partition.
Exemple L'empreinte $\langle ttSSS \rangle$ n'est pas un mode de l'empreinte pentatonique mineure $\langle tSStS \rangle$ et appartient donc à une autre famille, mais correspond bien à la même partition.
Combien y a-t-il de partitions différentes d'empreintes ? Pour le savoir, il suffit de connaître le nombre de partitions du nombre 12.
Résultat Il existe 77 partitions du nombre 12.
Le concept de partitions permet ainsi de réduire la complexité de 2048 empreintes en seulement 77 catégories. Pour terminer, complétons le tableau des répartitions des empreintes en fonction du nombre de notes avec les partitions :
| Notes $n$ | Empreintes $C_{11}^{n-1}$ | Familles | Partitions |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 11 | 6 | 6 |
| 3 | 55 | 19 | 12 |
| 4 | 165 | 43 | 15 |
| 5 | 330 | 66 | 13 |
| 6 | 462 | 80 | 11 |
| 7 | 462 | 66 | 7 |
| 8 | 330 | 43 | 5 |
| 9 | 165 | 19 | 3 |
| 10 | 55 | 6 | 2 |
| 11 | 11 | 1 | 1 |
| 12 | 1 | 1 | 1 |
Au niveau des partitions, ce sont donc les empreintes à 4 notes qui remportent la palme avec 15 partitions différentes.
Pour clôturer ce chapitre, on trouvera en annexes :
Concrètement, le tableau des partitions est outil permettant de naviguer facilement à travers les différentes empreintes. Nous pouvons par exemple ignorer les partitions contenant de nombreux chromatismes (B11, C10, D8, etc.) pour nous concentrer sur celles ayant un meilleur équilibre dans les intervalles.
Quant à la table des empreintes, celle-ci nous permet de voir concrètement à quoi ressemble une empreinte donnée ainsi que l'ensemble de ses modes.
↑Le candidat se donne souvent beaucoup de mal pour trouver la première équation fausse ; mais dès qu'il l'a obtenue, ce n'est plus qu'un jeu pour lui d'accumuler les résultats les plus surprenants, dont quelques-uns même peuvent être exacts. Henri Poincaré, Science et méthode (1908)
Dans le chapitre précédent, nous avons vu comment se répartissent les empreintes en fonction de leur nombre de notes et j'ai également proposé un classement par famille et par partition. Ce faisant, nous avons mis en évidence le fait que certaines empreintes génèrent moins de modes qu'elles n'ont de notes.
Dans ce chapitre, j'explorerai certaines propriétés des empreintes liées à leurs intervalles. Cependant avant d'entamer cette exploration, je souhaiterais attirer l'attention du lecteur sur les limites de l'approche abstraite et mathématiques de la musique développée dans cet essai.
Comme toute première hypothèse de cet essai, j'ai posé qu'il existait 12 éléments distincts format une liste circulaire ordonnée avec un sens de parcours privilégié. J'aimerais maintenant insister sur le fait qu'il n'existe a priori pas de lien entre ce modèle et tout phénomène physique lié à la musique. À place d'utiliser les noms de notes, j'aurais pu utiliser n'importe quels autres labels pour ces éléments sans changer aucunement les résultats dérivés précédemment. Les propriétés abordées dans cet essai sont en réalité des propriétés que présenteraient tout système analogue à 12 éléments.
C'est seulement parce qu'il existe 12 notes dans notre système musical occidental (simplifié) que nous pouvons a posteriori établir une correspondance entre ce modèle abstrait et la réalité musicale.

La mise en garde est donc la suivante :
Ce n'est pas parce que nous dérivons un résultat dans notre système abstrait, mathématiques, que celui-ci a forcément du sens d'un point de vue musical.
En effet, dans la suite de ce chapitre, je vais m'intéresser à certaines propriétés des empreintes, comme par exemple l'auto-similarité de leurs intervalles. Une empreinte symétrique par exemple, même si elle est esthétique du point de vue de ses intervalles, n'est pas forcément esthétique à l'oreille. En effet, nous avons plutôt tendance à entendre des notes dans un contexte, que des enchaînements d'intervalles. Par exemple, il peut être difficile de repérer une mélodie rétrograde, ou d'apprécier une pièce dodécaphonique, même si celles-ci sont élégantes sur la partition et relèvent de considérations ingénieuses. Il convient donc d'être critique par rapport aux considérations abstraites pour éviter de tomber dans leur piège classique : la déconnexion par rapport au réel.
Il faut donc envisager la suite de ce chapitre, et de manière plus globable cet essai en entier, à l'instar de la théorie des nombres en mathématiques : une exploration entreprise pour son propre intérêt intrinsèque, avec peut-être, mais pas forcément, des applications musicales concrètes à la clé.
Tout comme l'empreinte chromatique, certaines empreintes possèdent la propriété intéressante de ne faire entendre qu'un seul intervalle et sont donc formées par la répétition d'un intervalle unique jusqu'à atteindre l'octave.
Définition Je qualifie de monovalente5 une empreinte formée par la répétition d'un seul intervalle.
En plus de la gamme chromatique, il y a 5 autres empreintes qui possédent cette propriété6. Les voici:
| A1 | 0000 | 000 | 1v | $U$ | |||||||||||
| A2 | 0032 | 032 | 1v | 4a | $Q^2$ | ||||||||||
| A3 | 123 | 0136 | 1v | 3M | 6m | $T^3$ | |||||||||
| A4 | 219 | 0292 | 1v | 3m | 4a | 6M | $t^4$ | ||||||||
| A6 | 320 | 0682 | 1v | 2M | 3M | 4a | 6m | 7m | $S^6$ | ||||||
| A12 | 350 | 2047 | 1v | 2m | 2M | 3m | 3M | 4j | 4a | 5j | 6m | 6M | 7m | 7M | $s^{12}$ |
Puisque les empreintes monovalentes ne sont formées que d'un seul intervalle, celles-ci ne possédent qu'un seul mode et sont donc l'unique membre de leur famille. Il s'agit d'un premier exemple d'empreintes dont le nombre de modes n'est pas égal au nombre de notes.
Concernant l'instanciation d'une empreinte monovale à une empreinte concrète, notons qu'il n'existe que $\frac{12}{n}$ gammes à notes distinctes issues d'une empreinte monovalente à $n$ notes.
Exemple Pour la gamme par ton entier, il n'existe que $\frac{12}{6} = 2$ gammes à notes distinctes.
Mis à part les empreintes monovalentes, quelles sont les autres empreintes dont le nombre de modes est différent du nombre de notes ?
Définition Je qualifie de cyclique une empreinte dont le nombre de modes est strictement inférieur au nombre de notes.
En raisonnant un peu, on se rend compte que pour qu'une empreinte satisfasse cette condition, il est nécessaire que les intervalles de celle-ci présentent une forme d'autosimilarité, par exemple qu'elle soit formée par la répétition d'une suite d'intervalles.
Exemple L'empreinte $\langle tSs tSs \rangle$ est cyclique. Elle est en effet formée par deux répétitions de la suite d'intervalles « $tSs$ » et ne possède que 3 modes distincts:
En plus des 6 empreintes monovalentes, il y a 33 autres empreintes réparties en 11 familles qui sont cycliques. Voici leur répartition:
| Partition | Famille | Modes | Exemple |
|---|---|---|---|
| F4 | 093 | 2 | $(q s)^2$ |
| L4 | 145 | 2 | $(T S)^2$ |
| I6 | 274 | 2 | $(t s)^3$ |
| M8 | 340 | 2 | $(S s)^4$ |
| E6 | 194 | 3 | $(T s s)^2$ |
| N6 | 255 | 3 | $(t S s)^2$ |
| N6 | 280 | 3 | $(t s S)^2$ |
| G9 | 345 | 3 | $(S s s)^3$ |
| D8 | 306 | 4 | $(t s s s)^2$ |
| M8 | 333 | 4 | $(S S s s)^2$ |
| C10 | 348 | 5 | $(S s s s s)^2$ |
On notera qu'une manière de former ces empreintes cycliques consiste à partir d'une empreinte monovalente et à partitionner ses intervalles.
Exemple L'empreinte $\langle qs \rangle^2$ est une partition de l'empreinte monovalente $\langle Q^2 \rangle$. En effet $Q = q + s$.
↑Je vais maintenant m'intéresser à un autre type d'autosimilarité remarquable dans une empreinte.
Définition Je qualifie de symétrique une empreinte dont la suite d'intervalles présente une symétrie centrale.
Exemple L'empreinte $\langle T s S s T \rangle$ est symétrique.
Les empreintes symétriques sont donc des empreintes dont la suite d'intervalle est un palindrome. Mis à part les empreintes monovalentes qui sont trivialement symétriques, voici un tableau des partitions générant des empreintes symétriques, ainsi que le nombre généré par chacune :
| Partition | # | Exemple |
|---|---|---|
| B3 | 1 | s $\bar{S}$ s |
| B5 | 1 | s s $\bar{T}$ s s |
| B7 | 1 | s s s Q s s s |
| B9 | 1 | s s s s T s s s s |
| B11 | 1 | s s s s s S s s s s s |
| C10 | 5 | s S S s s S S s |
| D8 | 4 | s s t s s t s s |
| E6 | 3 | s T s s T s |
| F4 | 2 | q s s q |
| G3 | 1 | S $\bar{T}$ S |
| G5 | 2 | S s Q s S |
| G7 | 3 | S s s T s s S |
| G9 | 4 | S s s s S s s s S |
| H7 | 3 | s t s S s t s |
| I3 | 1 | t Q t |
| I5 | 2 | t s T s t |
| J5 | 2 | T s S s T |
| L3 | 1 | q S q |
| L4 | 2 | T S S T |
| L5 | 2 | S t S t S |
| M8 | 6 | S s s S S s s S |
| N6 | 6 | t S s s S t |
| P5 | 1 | S S T S S |
| P7 | 3 | S S s S s S S |
Soit un total de 59 empreintes symétriques.
↑Nous pouvons également mettre en évidence des relations de similarité entre différentes empreintes.
Définition Deux empreintes sont dites miroir l'une de l'autre si la suite d'intervalles de l'une est une symétrie réflective des intervalles de l'autre.
Exemple L'empreinte ionienne $\langle SSsSSSs \rangle$ et l'empreinte phrygienne $\langle sSSSsSS \rangle$ sont des empreintes miroirs.
Enfin plutôt que de comparer les empreintes par rapport à leurs intervalles, nous pouvons également nous intéresser à leurs notes fonctionnelles.
Définition Si une empreinte à n notes contient l'ensemble des notes d'une autre empreinte à plus de n notes, on dit que la première sous-tend la seconde, et que la seconde étend la première.
Exemple L'empreinte pentatonique mineure sous-tend l'empreinte mineure naturelle. Conversément, l'empreinte mineure naturelle peut être vue comme une extension de l'empreinte pentatonique mineure. Elle est formée en ajoutant deux notes supplémentaires, 2M et 6m, à l'empreinte pentatonique mineure :
| 1v | 2M | 3m | 4j | 5j | 6m | 7m |
Mentionnons que l'empreinte chromatique étend trivialement toutes les autres empreintes, et que l'empreinte à une seule note sous-tend trivialement toutes les autres.
↑Ici se conclue la première partie de cet essai qui en expose les fondements, à savoir la théorie des empreintes, leur dénombrement ainsi que leurs propriétés.
La prochaine étape consiste maintenant à explorer concrètement les différentes empreintes et répertorier lesquelles sont intéressantes musicalement, en les liant notamment aux noms de gammes usuels. La partition P7 par exemple contient la famille majeure (324) ainsi que la famille mineure mélodique (322). Tandis que la partition M7 engendre la famille mineure harmonique (288).